在评估不同销售频率的预测准确性时,如果没有对概率预测和观察到的实际数据进行适当分组,就会出现事后选择偏差。一方面,事后选择偏差是一个阴险的陷阱,它会诱导你对某个概率预测的偏差得出错误的结论--在最坏的情况下,让你选择一个更差的模型而不是更好的模型。另一方面,它的解决和解释涉及统计基础,如样本代表性、概率预测、条件概率、均值回归和贝叶斯法则。此外,它还让我们反思我们对预测的直觉期望,以及为什么这种期望并不总是合理的。
预报可以涉及离散的类别--明天会有雷雨吗?- 或连续量- 明天的最高气温是多少?我们在此重点讨论一种混合情况:例如,离散数量可以是某天售出的 T 恤衫数量。这样的销售数字是离散的,可以是 0、1、2、13 或 56;但肯定不是-8.5 或 3.4。我们的预测是概率性的,并不假装确切知道会卖出多少件 T 恤。一个现实的、但目标狭窄的(即精确)的概率分布是泊松分布。因此,我们假定我们的预测会产生我们认为推动实际销售过程的泊松率。
一个相当平庸的预测?
假设预测已发布,真实销售额已收集,并通过此类表格对预测进行评估:
| 观察到的销售频率 | 平均观察销售额 | 平均预测值 |
| 慢 0、1、2、件/天 | 0.804 | 1.373 |
| 中型 3-10 件/天 | 5.119 | 4.601 |
| 快速 >每天 10 件 | 13.880 | 11.041 |
数据按观察到的销售频率分组:我们将所有销售次数较少(0、1 或 2 次)、中等(3 至 10 次)或较多(10 次以上)的 T 恤天数分组。乍一看,这张表毫不含糊地喊道:"慢销产品预测过高,快销产品预测过低"。预测明显存在严重缺陷,我们会立即着手修正它,不是吗?
实际上,一切都很好,而且可能出人意料。是的,慢销品确实被高估了,而快销品则被低估了,但预测的表现恰如其分。我们的期望--"观察到的平均销售额 "和 "平均预测值 "两栏应该相同--是有缺陷的。我们要解决的是心理问题,是我们不切实际的期望,而不是糟糕的预测!概率预测从未承诺过,也永远不会实现,对于每一组可能的结果,预测的平均值与平均结果相吻合。
让我们来探讨一下为什么会出现这种情况,如何圆满解决这个难题,以及如何避免类似的偏见。
我们究竟要求什么?
让我们后退一步,用语言表达表格所揭示的内容。我们使用实际观察到的销售额对数据进行分级,也就是说,我们根据观察到的销售额在一定范围内(慢销、中销或快销)对预测结果和观察结果进行过滤或设定条件。第一行包含 T 恤售出 0 次、1 次或 2 次的所有天数,中间一列为我们提供了信息:

即我们将所有值为 2、1 或 0 的观测值归入其中的观测值桶的平均值--肯定是介于 0 和 2 之间的数字,恰好是 0.804。右侧一栏是对同一批观测数据的预期平均值预测、

也就是说,对于所有 2 或小于 2 的观测值,我们提取相应的预测值,然后计算所有这些预测值的平均值。
先验地讲,我们没有理由让第一个表达式和第二个表达式取相同的值,但我们直觉地希望它们取相同的值:期望平均预测值等于平均观测值似乎并不过分,不是吗?
| 观察到的销售频率 | 平均观察销售额 | 平均预测值 |
| 慢 0、1、2、件/天 | E (observation | observation ≤ 2) | E(预测值 | 观测值 ≤ 2) |
| 中型 3-10 件/天 | E (observation | observation ≤ 3, ≤ 10) | E (预测值 | 观测值 ≤ 3, ≤ 10] ) |
| 快速 >每天 10 件 | E (observation | observation ≥ 11) | E(预测值 | 观测值 ≥ 11]) |
前瞻性预测,后顾之忧
根据其词源,预测具有前瞻性,为我们提供了观察未来结果的概率、
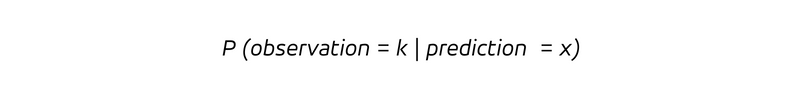
即在预测率为 x 的情况下,观察到结果 k 的条件概率。由于我们有一个条件概率,所以我们要考虑假设预测值为 x 的观测值的概率分布。对于无偏预测,以预测值 x 为条件的观测值的期望值,即在预测值 x 的假设条件下的平均观测值:
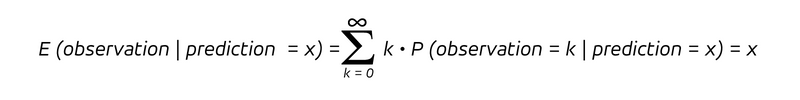
这正是任何无偏预测所承诺的:将所有预测值 x 相同的预测分组,所得观测值的平均值应接近这个值 x。虽然分布可以呈现出多种不同的形状,但这一特性至关重要。
让我们回过头来看看表格:我们在左栏所做的不是按预测分组/条件分组,而是按结果分组/条件分组。因此,右侧一栏提出的是 "在某一结果 k 的情况下,我们的平均预测值是多少 "这样的后向问题,而不是 "在我们预测 x 的情况下,平均结果会是多少 "这样的前向问题。
为了用前瞻性声明来表达后瞻性声明,我们运用了贝叶斯法则、

前瞻性问题和后瞻性问题不同,答案也不同:出现了其他术语 P(预测 = x)和 P(观察 = k),即预测和结果的无条件概率。因此,在结果一定的情况下,平均预测值的期望值变为

简约范例
E (prediction | observation = m)的值是多少?为什么不简化为观测值 m 呢?
在绝大多数情况下,E (prediction | observation = m) ≠ m成立。让我们来看看为什么!
考虑一件每天销量相同的 T 恤衫,该 T 恤衫的销量是泊松分布,比率为 5。每天的预测值都是 5。然而,结果却各不相同。显然,5 是对结果 4 及以下的高估,而对结果 6 及以上的低估。如果我们再按结果分组,就会遇到这样的情况:
| 观察到的销售频率 | 平均观察销售额 | 平均预测值 |
| 慢 <每天 5 件 | 3.0082 | 5 |
| 中型 每天 5 件 | 5 | 5 |
| 快速 >每天 5 件 | 7.2844 | 5 |
从该表中我们再次得出结论,滞销日的预测过高,而畅销日的预测过低,事实也确实如此。由于预测值总是 5,因此对每个观测值E (预测值 | 观测值 = m) = 5 都成立。
预测仍然 "完美"--结果与预测完全一致,它们遵循率为 5 的泊松分布。预测不足和预测过度的印象完全是数据选择的结果:通过选择高于 5 的结果,我们保留了高于预测值 5 的结果,这些结果被低估了;通过选择低于 5 的结果,我们保留了低于预测值 5 的事件,这些事件被高估了。就概率预测而言,有些结果预测不足,有些结果预测过高,这是不可避免的。通过预期预测无偏,我们预期在给定预测值 m 的情况下,预测不足和预测过高的情况是平衡的。我们不能期望的是,当我们主动选择预测过高或预测过低的观测值时,这些观测值分别不会被预测过高或预测过低!
在现实情况中,我们不会处理每天都假设相同值的预测,但预测本身会有变化。不过,选择 "相当大 "或 "相当小 "的结果相当于将预测不足或预测过高的事件保留在桶中。因此,一般情况下E(预测 | 观察 = m)≠ m。更确切地说,当 m 大到选择它就等于选择了预测不足的事件时,我们就会有E (prediction | observation = m)< m;当 m 小到选择它就等于选择了预测过度的事件时,E (prediction | observation = m)> m。
确定性预测--你本该知道,一直都是!
为什么我们会感到困惑呢?为什么我们会对平均观测值与平均预测值之间的差异感到不安呢?我们的直觉依赖于预测和观察的平等,这是确定性预测的特点。在概率语言中,确定性预测表示:P(观测 = 预测)= 1 和 P(观测≠预测)= 0:P(观测值 = 预测值)= 1和P(观测值≠预测值)= 0
预测者认为观测结果将与她的预测完全吻合,即预测值和观测值重合的概率为 1(或 100% ),而所有其他结果都被认为是不可能的。这是一种自信,不能说是一种大胆的说法。用条件概率来表示,我们可以总结一下:

换句话说,只要我们预测会卖出 k 件(竖条后的条件),我们就会卖出 k 件。由于确定性不仅意味着我们每次预测 k 时都会观察到 k,还意味着每次观察到的 k 都是事先被正确预测为 k 的,因此我们有
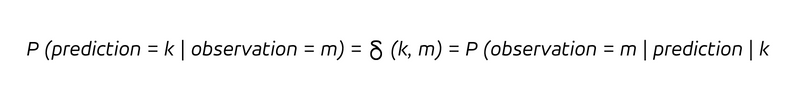
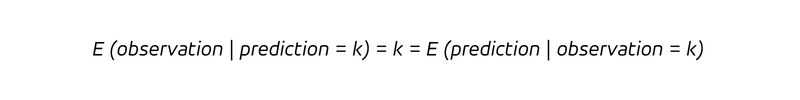
决定论使得后瞻性问题和前瞻性问题之间的区别变得不再重要。对于确定性预测,我们不会通过观察结果学到任何新东西(我们已经知道了!),也不会更新我们的信念(我们的信念已经是正确的了)。
在这种确定性预测中,所有出现的概率分布都会在唯一可能的结果处坍缩到 100% 的峰值,因此不会出现事后选择偏差--我们假装事先完全知道,所以我们应该知道--在任何情况下都是如此。如果测量结果并非如此,那么你的 "确定性 "预测就是错误的。
每一个严肃的预测都是概率性的
与确定性预测相比,概率性预测的表述更弱,而且对于概率性预测,我们必须放弃 "平均预测每个结果 m 为 m "的想法--因此,确定性预测似乎非常有吸引力。但是,以确定的方式预测每天的 T 恤销售量是否现实?假设你能预测明天的 T 恤销量为 5 件。也就是说,你能说出五个人,无论发生什么(意外、疾病、雷雨、突然改变主意......),明天都会买一件红色 T 恤。我们怎么能指望达到如此确定的程度呢?你曾经那么确定第二天会买一件红色 T 恤吗?即使有五个朋友承诺,在任何情况下,他们明天都会买一件 T 恤,你怎么能排除其他所有潜在客户中的其他人也会买一件 T 恤呢?除了某些非常特殊的边缘情况(客户极少、库存量远小于真实需求量)外,以确定性的方式预测物品的确切销售数量是不可能的。不确定性只能在一定程度上得到控制,任何现实的预测都是概率性的。
评估卫生
还有另一种方法来反驳表 1:通过建立表格,我们提出了一个统计问题,即预测是否存在偏差,以及偏差的方向(我们暂且忽略统计意义的问题,假设我们看到的每个信号都具有统计意义)。与任何统计分析一样,预测分析也会出现偏差。我们根据结果进行选择的方式就是选择偏差的一个典型例子:慢速卖家"、"中速卖家"、"快速卖家 "组中的事件并不能代表整组预测和观察结果,但我们把它们分成了预测不足和预测过高两组。此外,我们在预测评估中使用了所谓的 "未来信息":我们将预测和观测结果归类的桶在预测时尚未确定,但它们是事后确定的。因此,我们这样设置表格违反了统计分析的基本原则。
回归均值
我们刚刚遇到的现象--极端事件并没有像预测的那样极端--与 "向均值回归 "直接相关,这是一种我们甚至不需要预测的统计现象:假设你观察到一个产品销售的时间序列,它没有表现出季节性或其他与时间相关的模式。当某一天的观察销售额大于平均销售额时,我们可以肯定第二天的观察销售额会小于今天的销售额,反之亦然。同样,由于过程的概率性质,我们选择一个非常大或非常小的值,很可能会选择一个正或负的随机波动,销售额最终会 "回归均值"。从心理学上讲,我们很容易将这种向平均值的回归--一种纯粹的统计现象--归因于某种积极的干预。
决议:按预测分组,而不是按结果分组。对选择偏差保持警惕。
解决这一难题的办法是什么?通过按结果分组,我们选择的是与其预测值相比 "相当大 "或 "相当小 "的值--我们得到的不是一个有代表性的样本,而是一个有偏差的样本。这种选择偏差会导致一些水桶分别包含自然 "相当低估 "或 "相当高估 "的结果。如果我们认为在 "慢速"、"中速 "和 "快速 "移动项目中,平均预测值和平均观测值应该是相同的,那么我们就会受到事后选择偏差的影响。我们必须忍受并接受两栏之间的差异。幸运的是,我们可以利用贝叶斯定理获得现实的期望值。因此,一种解决方案是在表格中另设一列,包含每个水桶平均预测值的理论预期值,可以与该水桶的实际平均预测值相对照。也就是说,我们可以量化并从理论上重现事后选择偏差,看看汇总数据是否符合理论预期。
然而,一个简单得多的解决方案是向数据提出不同的问题,即与预测承诺一致的问题。这样,我们就可以直接检查这些承诺是否兑现:我们不按结果分组,而是按预测分组,即按预测的慢销、中销和快销分组。在这里,我们可以检查预测的承诺(给定某个预测的平均销售额与该预测相符)是否实现。在我们的示例中,我们得到了这个表格:
| 预测销售频率 | 平均观察销售额 | 平均预测值 |
| 慢 <每天 3 件 | 1.288 | 1.267 |
| 中型 每天 3 件 | 5.247 | 5.229 |
| 快速 >每天 3 件 | 12.855 | 12.950 |
考虑到测量总数,统计显著性检验将是负值,即显示观察到的平均销售额与平均预测值之间没有显著差异。我们的结论是,我们的预测不仅在总体上是无偏的,而且在每个预测层也是无偏的。
一般来说,您可以通过过滤预测时已知的任何信息来评估预测,而且预测在所有测试中都应该是无偏的。然而,滤波器不允许包含未来信息,如观测中出现的随机波动,自然界只在预测时间点的未来决定这些信息。
如果你能走到这一步,你应该带走什么?(1) 按结果进行选择时,样本不具有代表性。(2) 对自己的期望持怀疑态度--看起来非常合理的直观期望最终会被证明是有缺陷的。(3) 明确自己的期望,并根据充分理解的案例进行测试。













