本故事分为两部分,分别讲述如何处理涉及快速和慢速商品的销售预测。 点击此处查看第一部分。
销售预测可以精确到什么程度?
波动抵消机制确保粒度低的预测比粒度高的综合预测更不精确、更嘈杂、更不确定:我们对一周椒盐脆饼总量的预测(相对而言)要好于对一天椒盐脆饼总量的预测。
到目前为止,我们已经定性地论证了这种关系,但我们能否定量地说明,对于不同的预测销售率,我们最理想的预期精确度是多少?值得庆幸的是,这确实是可能的,而且是以一种普遍的、与行业无关的方式实现的。我们在上一篇关于预测评估中的 "后见之明偏差 "的博文中指出,完全确定的预测是不现实的:让我们来看看上面关于 5 个椒盐脆饼的预测。就单个客户而言,确定性预测 5 意味着 5 个客户无论如何都会在预测日购买椒盐卷饼。但是,我们不仅要假定对这 5 位顾客非常了解(也许比他们自己还了解,谁没有自发地决定买或不买椒盐脆饼呢?这种确定性显然是不可能的。考虑到一些不确定性,比如 6 个顾客每人购买一个椒盐脆饼的概率为 5/6=83.3% ,结果就是数学家所说的椒盐脆饼销售总量的二项分布:卖出 6 个椒盐脆饼的概率是 (5/6)^6,一个也卖不出去的概率是 (1/6)^6,卖出 1 到 5 个椒盐脆饼的概率包含各自的二项式系数。然而,要知道有 6 个客户很可能会购买,这仍然是不现实的。即使假设 10 位顾客每人购买一个椒盐脆饼的概率为 50% ,这也是一项挑战。我们可以继续前进,进一步增加潜在顾客的数量,同时降低他们购买椒盐脆饼的概率,沿着极限泊松分布的路径前进:在泊松极限分布中,我们假设客户群是无限的,每个客户的购买概率都微乎其微,而我们可以控制客户数量与购买概率的乘积:销售率。泊松分布的刻度是一致的:如果日销售额服从均值为 5 的泊松分布,那么周销售额服从均值为 35 的泊松分布。泊松分布是销售预测的 "黄金标准":我们假定知道影响特定产品销售的所有因素,但无法获得个人客户数据,从而无法对个人客户的购买行为做出更有力的说明。当预测精度达到泊松分布的预期水平时,通常就已经达到了预测的极限。
泊松分布只包含一个参数,即销售率;分布宽度,即平均值周围可能结果的分布,完全由其函数形式决定,这反映了自洽性。也就是说,可达到的精确度只取决于所考虑的时间间隔内的预测销售率:每天预测 5 个椒盐脆饼的销售量与每周预测 5 个生日蛋糕、每小时预测 5 个馒头或每季度预测 5 个婚礼蛋糕的销售量的分布相同。换句话说:最佳情况下可达到的相对误差完全且唯一地由预测值本身决定!
为什么不能可持续地提供超新鲜滞销品?
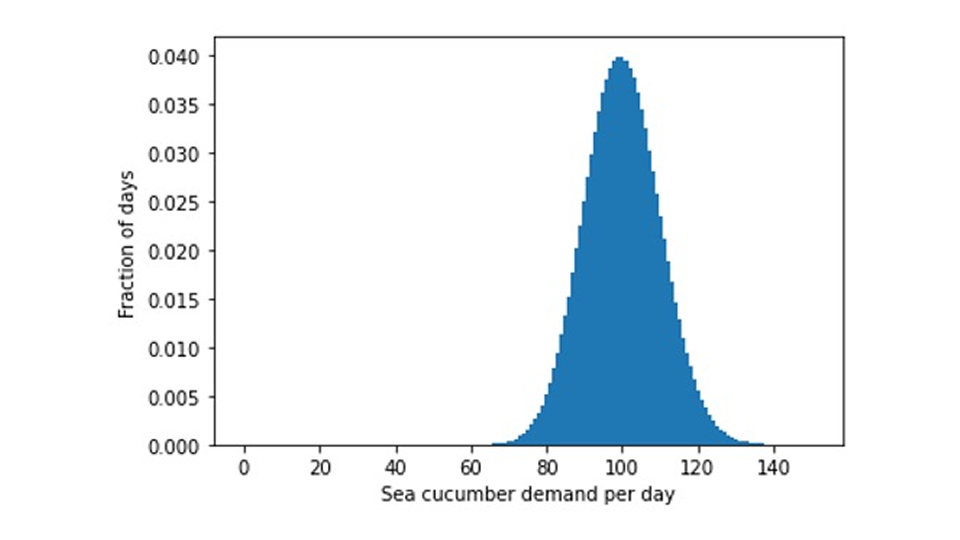
有了对误差缩放的这一认识,让我们回到为什么新鲜海参不是在世界各地都有供应的问题上来:我们展示了对每天一只海参的完美泊松预测的日销售量预期分布:

我们会经历 37% 天没有任何需求,37% 天会有一个海鲜爱好者想买一只生海参,26% 天会有两只甚至更多的需求。如果没有人买海参,我们必须在一天结束时将其扔掉,那么我们应该储备多少海参?如果我们有一块存货,那么在 37% 天内,我们就不得不把它扔掉,而在 26% 天内,我们就会有顾客不高兴,因为他们买不到他们想买的海参。有了两件存货,我们需要在 74% 天后扔掉至少一件--鉴于海参在许多地方都受到保护,这真是一种浪费!显然,以满足极小的生海参需求为目标的商业模式是不可行的,只有在利润极高的情况下才能维持下去:买生海参的人需要补贴所有不卖海参的日子--而这些人即使想吃海参,也不一定能吃到!在对利润率和处理成本作温和假设的情况下,超新鲜超低速销售商的正确库存量是:零。
同样,这都是非比例缩放造成的:每天预测 100 个鲜海参的预期销售分布不仅是上述每天 1 个海参的预期销售分布的夸大版,而且其形状也不同--就像大象不像大黑斑羚一样:
对于那些希望在釜山买到椒盐脆饼或在北欧买到更多种类水果的人来说,这无疑是个坏消息!不过,希望还是有的:当一种易腐烂的菜肴成为一种流行时尚,当需求超过了一定的临界点,这种新奇的食物就能在新的地方立足--几乎在地球上的任何地方都能吃到美味的寿司。
综上所述,由于预测误差的非比例缩放,即使假设预测完美无缺,当销售率下降时,产品的超储和库存不足也会不成比例地增加。因此,只有在每个保质期的销售率超过一定水平时,才有可能持续提供某种易腐食品。
评估预测误差
现在,我们已经明白了为什么不能指望在国内找到国外的新鲜美食,现在让我们为负责判断预测质量的数据科学家和商业用户总结一些经验:对于高预测销售率而言,使真实销售值相对于预测平均值上升或下降的随机波动不能作为任何重大偏差的借口,我们可以将这种偏差归因于预测中的实际错误或问题。我们上面讨论的统计特异性并不重要。如果预测的总需求量为 1'000'000,而总销售量为 800'000,那么这个 20% 的误差不是由于不可避免的波动造成的,而是由于预测偏差造成的。
对于较小的预测数字,我们无法再明确地将观测到的偏差归因于预测错误:在预测值为 1 的情况下,观测值 0(偏离 100% )很有可能发生(概率为 37% ),观测值 2(偏离 100% )也很有可能发生。判断预报的好坏变得难上加难,因为自然基线、不可避免的噪音占据了主导地位。
那么,我们是否应该将我们的预测分为 "快卖者 "和 "慢卖者",对于 "快卖者",我们将观察到的偏差归因于预测误差,而对于 "慢卖者",我们则更为仁慈?我们建议不要这样做:那么中间的情况呢?慢 "和 "快 "的界限在哪里?如果一个产品变得稍微受欢迎,如果它越过了这个界限,它的预测质量判断突然跃升怎么办?在 "快 "和 "慢 "之间有一个连续的过渡,没有自然的边界,我们可以从这幅预测的预期相对误差与预测值的函数关系图中看到这一点(请注意腹坐标上的对数刻度,以及我们使用最佳点估计器计算预期误差,该估计器不是泊松分布的平均值,而是中位数):
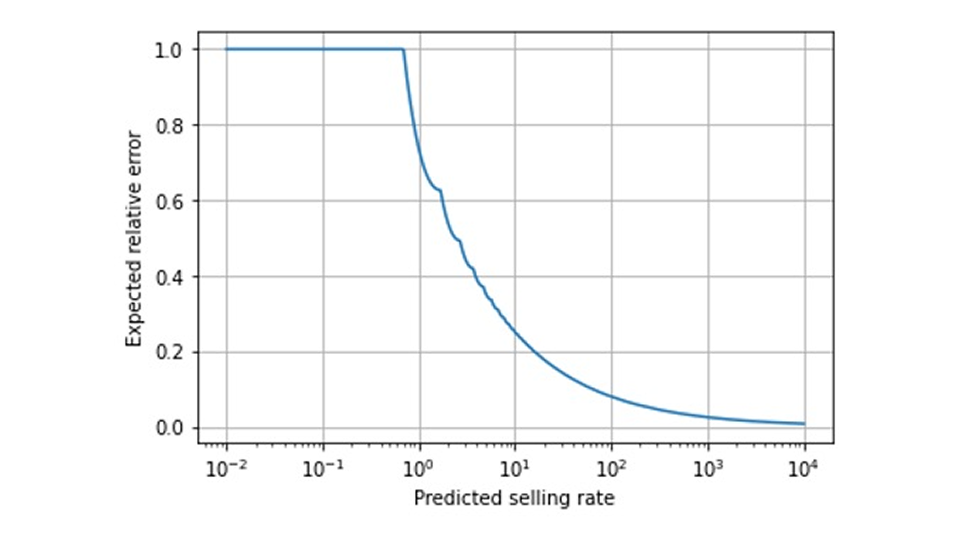
由于这种连续的转变,我们建议按预测率进行分层评估,即把预测值相似的预测值分成若干个分区,并分别评估每个分区的误差指标。我们 之前 关于 "后见之明偏差 "的 博文 解释了为什么要根据预测值而不是观察到的销售额进行分选,尽管后者比前者更自然。对于每一个分段,我们判断预测精度是符合理论预期(如上图所示),还是存在较大偏差。我们对预测的期望值应取决于预测率:对于极小值(小于 0.69),大部分观察到的实际销售额为 0,而我们基本上 "总是完全偏离",误差为 100% - 这是不可避免的。如果预测的销售率为 10,那么在最好的情况下,我们将不得不忍受 25% 这一可怕的相对误差!当我们预测 100=10^2 时,预计相对误差仍为 8% 左右,而预测速率为 1'000=10^3 时,误差降至 2.5% 。因此,要求将所有销售率的误差临界值定为 10% 会适得其反:绝大多数慢速销售者都会违反这一临界值,并为找出 "预测失误 "的原因而耗费资源,而那些遵守临界值的快速销售者仍有可能得到一些改进,因此不会受到关注。
在实践中,与上述理想线的偏差取决于预测范围(是明天还是明年?)我们是在预测一种著名的非季节性杂货,还是在预测一种介于时髦与无味之间的非常规精致服饰?尽管如此,考虑到预测误差的普遍非比例缩放性是预测评估方法应满足的最重要方面!
避免天真的扩大规模陷阱,接受并战略性地处理滞销噪音
除了把参观当地餐馆列入下一次度假的必做清单之外,您还应该从这篇博文中得出什么结论呢?
确保您在评估中设定的时间聚合规模与业务决策的时间规模相匹配:由于草莓和海参的生长期只有一天,因此计划的生长期也是一天,以日为单位进行评估是合适的。你不能用昨天的过剩库存来弥补今天的草莓需求,反之亦然。对于使用寿命较长的物品来说,商业决策中的错误真正体现出来的时间肯定不是一天:如果一件衬衫周一没有买到,可能周二或两周后才会买到,这对于每月都要订购的衬衫存货来说并不重要。如果您在评估中遇到许多预测数量较小的项目 (<5),请仔细检查后者是否真的是相关的项目,并据此做出购买、补货或其他决定。
不要为整个产品组合的预测精度设定固定目标,无论是绝对目标还是相对目标:销售速度快的产品很容易达到较低的相对误差,而销售速度慢的产品则似乎很难达到。取而代之的是,将您的预测分为预测值相近的桶,并分别对每个桶进行判断。设定一个现实的、取决于销售率的目标。
对于滞销品销售商来说,必须意识到预测的概率性质,并从战略上考虑到不可避免的巨大噪音,无论是在不易变质的商品上采用安全库存启发式方法,还是在婚礼蛋糕等商品上采用按订单生产的策略。
虽然慢销品不可避免的预测误差可能会令人恼火,但令人鼓舞的是,预测技术的局限性可以通过严格的方式定量确定,这样我们就可以在商业决策中对其进行战略性考虑。













