由于平均绝对误差的定义简单,与业务的相关性直观,因此在评估模型时,平均绝对误差是从业人员的首选。相比之下,"排名概率得分"这一评价指标乍看之下并不迷人:它的名字很有威慑力,其正式定义也很繁琐,因此几乎没有供应链从业人员知道它,更不用说使用它了。但他们错过了!概率排序得分是平均绝对误差在概率预测领域的自然延伸,也就是 "知道 "自身不确定性的预测。它具有直观的解释,解决了平均绝对误差的几个严重问题。排序概率得分比平均绝对误差更能反映业务,它考虑了统计的不确定性,从而协调了象牙塔中的统计理论与日常实践。
合理的商业标准:平均绝对误差
"我们应该用哪个指标来评估需求预测模型?
这个问题通常用"平均绝对误差 "来回答,而且理由相当充分。绝对误差 (AE) 通常合理地反映了预测 "偏差 "的成本:当我预测要卖出 8 篮草莓,储备了 8 篮,但实际需求是 9 篮时,我的绝对误差为 1,1 个不满意的客户会转向竞争。当我的预测是 11 筐草莓,而需求量是 9 筐草莓时,AE 是 2,我有 2 筐草莓要处理。对于观察到的结果 9,下图中的蓝线表示 AE 与预测值的函数关系:
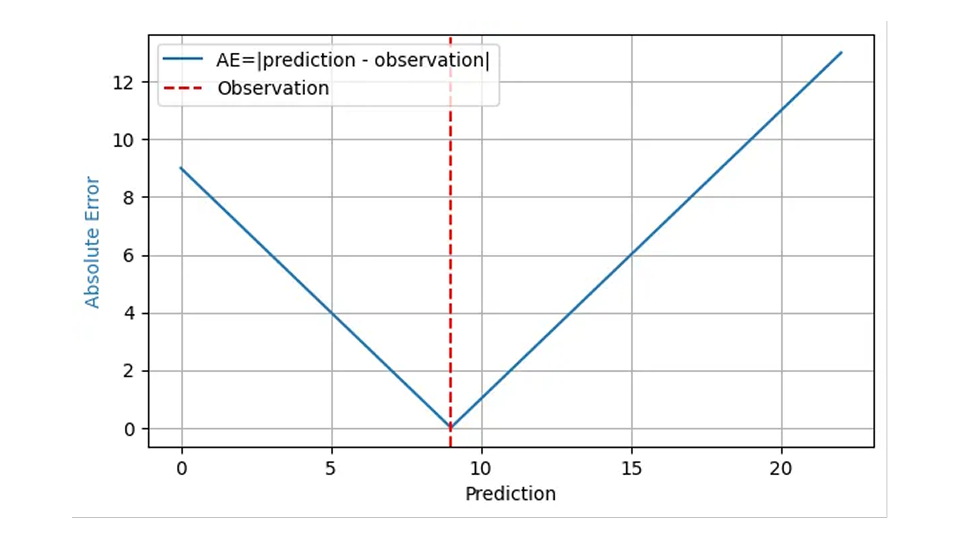
由于预测误差的财务影响通常与预测误差本身成正比,因此,许多预测和结果的平均绝对误差(MAE)反映了业务成本,至少在一个超量库存与一个库存不足具有相同财务影响的假设下是如此。平均平方误差 (MSE) 是指误差越大,"偏差 1 "的代价就越高,这在商业中是不现实的。平均绝对百分比误差(MAPE)是归一化 AE 的平均值,即平均值(AE/观测结果),它存在严重的意外隐患(如上一篇博文所述),在需求预测中可以放心地不予考虑。
因此,建议实践者使用 MAE 或其归一化变体相对 MAE(RMAE = MAE / Mean(outcome))作为评估模型的首选简单方法。不过,MAE 和 RMAE 的典型值与规模有关:与某些特殊电池(滞销电池)的预测相比,瓶装牛奶(快销)的预测自然会有更大的 MAE 和更低的 RMAE。诚然,要看到这一点并不容易,这也是为什么专门针对这一问题的博客投稿甚至没有写成一篇文章,而是分成了《预测少有不同》的第一部分和第二部分。
既然 MAE 简单易懂、广为人知且具有相关性,为什么还要撰写或阅读关于替代品的博文呢?那么,盲目相信评价指标无疑是最不科学的数据之一。让我们对 MAE 进行一次彻底的深入研究,看看它的行为是否真的像我们想象的那样,如果不是,又该如何解决。长话短说:在评估 AE 时,你会遇到一些意想不到的、令人讨厌的复杂问题,但这些问题都可以通过一个相关但被低估的指标--"排名概率得分"--来轻松解决。
等等,没那么快!如何评估概率预测的平均绝对误差
到目前为止,我们假定 "预测 "只是一个数字,就像预测目标本身一样(售出商品的数量,可以是草莓篮、苹果、牛奶瓶或红色 T 恤衫的数量)。计算预测值(一个数字)和实际观测值(另一个数字)之间的差值根本不是问题:我预测会卖出 10 个苹果,卖出了 7 个,AE 是 3。无需统计学博士学位。
但这其中有一个微妙之处:如果我预测卖出的苹果数量是 10.4 个,而不是 10 个呢?我是如何决定手头的存货的?可能我还是会订购 10 个苹果,也就是说,预测中 0.4 的微小差异不会造成任何业务上的差异,业务结果还是一样的。然而,绝对误差会稍大一些,为 3.4,而不是 3。第一幅图中预测绝对误差的平滑表现是一种误导:预测值与实际值之间的差额并不是与业务相关的数量,而是订购数量与实际数量之间的差额。既然我知道只能出现整数,那我为什么还要预测除整数以外的其他数字呢?
造成这种差异(我们预测非整数值,但只测量整数量)的原因是,大多数预测都不是 "点预测",它表达的是对目标的普遍的、与评估无关的 "最佳估计",而是提供一种概率分布(不用担心:仍然不需要统计学博士学位)。它们告诉我们每种可能结果的可能性有多大:在预测 10.4 时,我们不会假定某个顾客会把苹果切成一块一块的去买 0.4 个苹果,但我们会认为 "11"、"12"、"13 "这些可能的结果比预测 10.0 更有可能出现。因此,预测不仅仅是可以与目标进行比较的数字,更是 一种功能 。尽管讨论适用于任何分布,但在本篇博文中,我将假设预测的概率分布是泊松分布(请查看我们的相关博文:这里和这里)。
请看这里,当我们预测 1.3、3.8 或 11.7 时,我们暗含了怎样的概率分布:
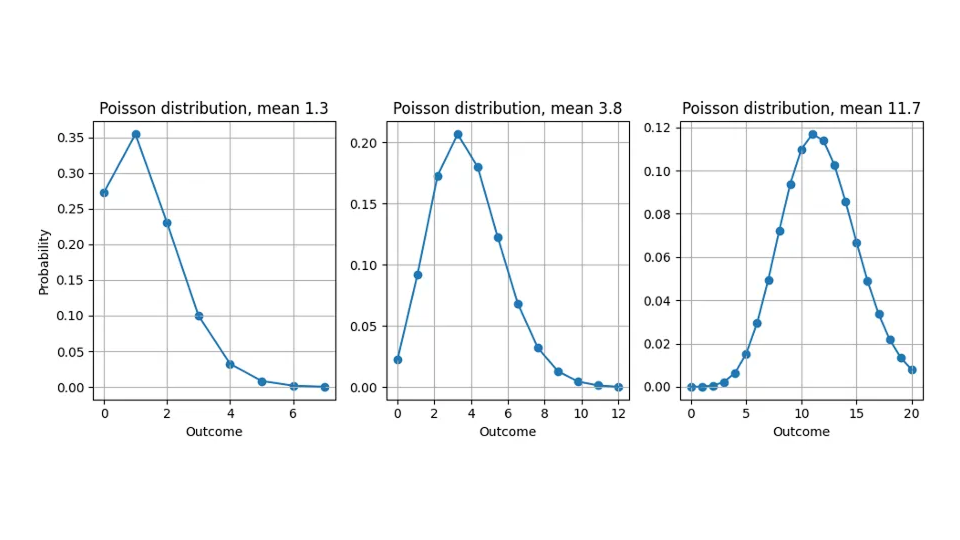
返回绝对误差的计算:如何从一个数字中减去一个函数?从概率分布中减去 7 件已售出的商品毫无意义。我们需要用一个数字来概括预测的概率分布,以便进行比较。这个汇总数被称为点估计值,然后可以从观测到的实际值中减去点估计值,得出误差。
概率分布可以用多种方式概括:平均值是最直接的方法,但也可以用最可能的结果(模式)、将概率分布分成两个相等的半数的结果(中位数)或其他方法来概括分布。
在点估计器的动物园里,有些点估计器感觉比其他点估计器更自然--我们能不能选择我们最喜欢的摘要呢?不,正确的点估计是由所选的评估指标决定的。换句话说:您可以选择哪种误差指标来评估我的预测(MAE、MAPE、MSE......),但随后由我来选择如何总结该评估的预测。我的 MAE 获胜点估计值与 MSE 获胜点估计值不同,更不用说 MAPE 了。这种选择可能听起来很武断,甚至可能不诚实,但它反映了概率预测的巨大表现力:它们所包含的信息远比单一的 "最佳猜测 "要多得多。根据评价的方式,以及误差指标对 "最佳 "的实际定义,可以相应地选择特定评价方法的优胜值。换句话说:只要不清楚如何定义 "最佳","给出你的最佳预测 "这个问题就毫无意义。一个单一的概率预测可以产生许多不同的点估计或 "最佳猜测",这取决于如何评估预测。
对于平方误差 (SE),点估计器是分布的平均值。对于绝对百分比误差 (APE),点估计器是一个非常反直觉的函数,我就不给大家添麻烦了,它导致了MAPE 评估中意想不到的悖论。
绝对误差需要的是分布中值,而不是平均值,是的,这很重要
对于 AE(绝对误差),正确的点估计结果是中位数。是的,是中位数,而不是平均数,不,我们不能只用平均数来代替。让我来解释一下为什么只有中位数才是 AE 的最佳值。我们来做一个预测,也就是一个分布,假设它是泊松分布,均值为 3.8,中位数为 4。结果必然是一个整数,不可能是 3.8。为了找到合适的股票数量,我们要选择一个估计值,使我们在观察该分布的结果时平均发现的 AE 越小越好。
我们要寻找合适的点估算器,将整个分布浓缩成一个数字,即操作上的最佳库存量。在本图中,我尝试了三种不同的估计值(3、4、5):
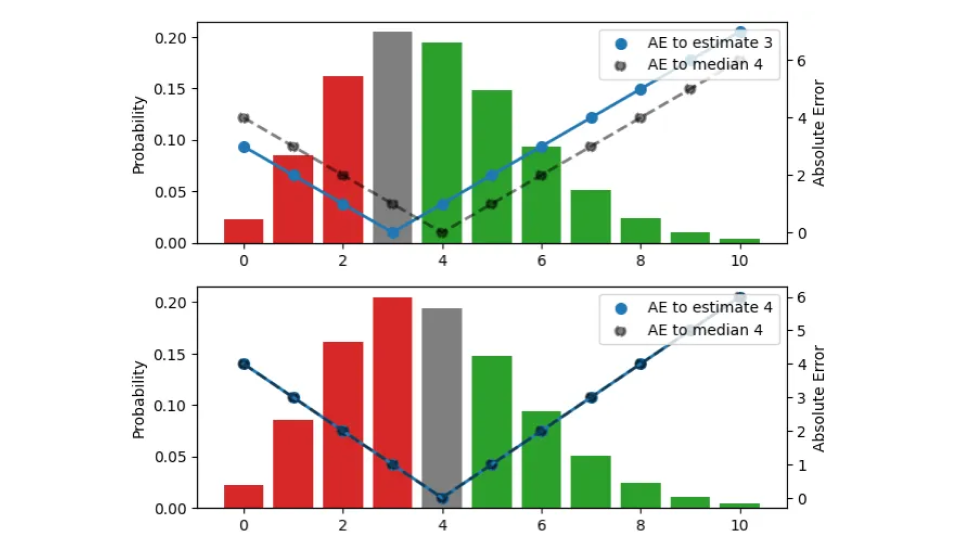

三幅图的概率分布(左侧比例尺)相同。上图显示的是估计值 3,中图显示的是估计值 4,下图显示的是估计值 5。估计值与结果之间的 AE 用蓝点表示,用实线连接(右标尺);与中位数 4 有关的 AE 用黑点表示,用虚线连接。例如,当估计值为 3 时(上图),结果 3 的误差消失,蓝色实线为 0。
条形图的颜色表示预测结果是比估计结果小(红色)还是比估计结果大(绿色),条形图的高度表示预测结果出现的概率。当结果与估计值一致时,误差为零,显示为灰色。通过将估计值向上移动一个单位,我们向下移动了一个板块,红色条下和灰色条下的所有观测值都会使新的移动估计值的误差增加一个单位:对于之前的估计值 3,结果 2 的误差为 1,而对于估计值 4,同样的结果误差为 2。另一方面,所有绿色条的观测值在移动后误差单位减少了一个:对于估计值 3,结果 5 的误差为 2,而对于估计值 4,误差减小为 1。
让我们来总结一下当估计值增加一个单位时会发生什么:对于那些小于或等于估计值的结果,分布下 AE 的预期值会增加(我们对它们的高估甚至超过了我们的高估),而对于那些大于估计值的结果,预期值会减少(我们对它们的低估减少了)。增量与红色和灰色条形图的总面积成正比,减量与绿色条形图的面积成正比。
完全类推,当估计值减少一个单位时,绿色条形图或灰色条形图下的观测值会各增加一个单位的误差,而红色条形图中的所有观测值会减少一个单位的误差。
对于给定的分布,将估计值上下移动 1 个百分点会增加或减少所产生的预期绝对误差,我们可以通过寻找最小值来搜索正确的点估计值。您可能已经总结出了这样一条经验法则:如果对于当前的估计,大多数结果都预测不足,那就降低估计值;如果大多数结果都预测过度,那就提高估计值。只有当与预测过高和预测过低相关的概率质量之差("红 "条和 "绿 "条的总面积之差)小于灰条时,误差才不会进一步增大。中图就是这种情况:该估计值的下方和上方的概率质点几乎重合,因此向任一方向移动都会增加总误差。这个估计值与中位数相符:当你得到一个概率分布时,绝对误差最小的点估计值在一半情况下会高于或低于结果。
我认为这一点值得强调,因为它经常被忽视:当 7.3 是对分布均值的最佳估计时,评估绝对误差与观测值(例如 9)的正确方法不是从 9 中减去 7.3,而是从 9 中减去该分布的中位数(泊松分布的中位数是 7)。令人惊讶的是,对股票决策的平均值进行精确估算并没有帮助,预测值是 7.1 还是 7.3 并不重要:您需要确定一个整数。然而,当把预测汇总到更高层次进行规划时,7.1 和 7.3 之间的区别就变得很重要了。
在你看来,平均值和中位数之间的这种区别可能有些肤浅:毕竟,将概率平均分成两半的值与该分布的平均值看起来非常相似,而且对于大多数良性分布(例如与零售业相关的泊松分布)来说,它们也很接近。然而,两个分布的平均值可能相同,但中位数可能不同;另外两个分布的中位数可能相同,但平均值可能不同。如果只是把平均值和中位数当作同义词来使用,就无法真正找到最佳预测。
平均绝对误差的意外缺陷
我们现在知道如何评估概率预测的绝对误差了:我们用估计点的中位数(我们会储备的物品数量)来概括分布,然后用观察结果减去中位数,求出绝对值。我试图用下面的图来直观地说明这一点:
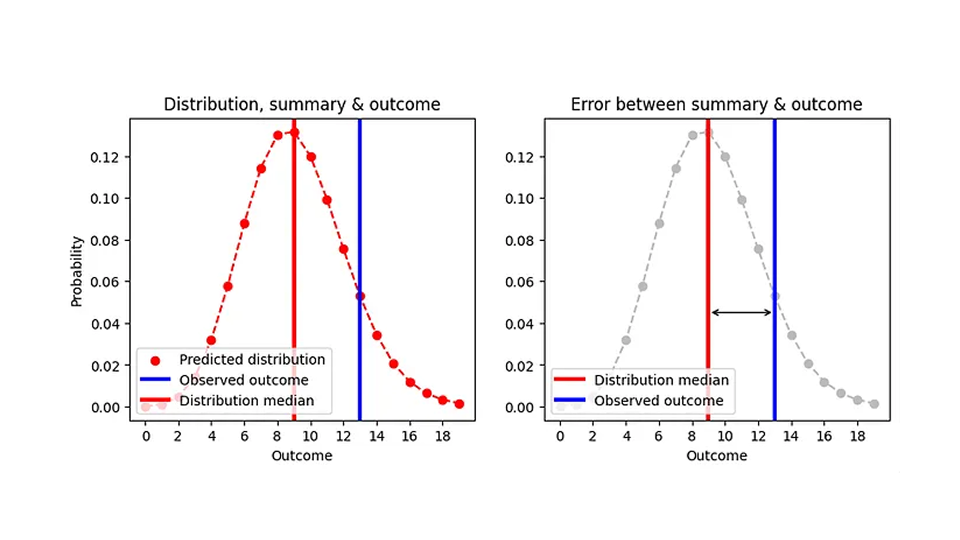
由于中位数总是整数,因此两个完全不同的分布可以产生相同的绝对误差。例如,波松预测值为 8.7(中位数=9)和波松预测值为 9.6(中位数=9)的 AE 值是相同的,尽管预测值明显不同,如图所示:
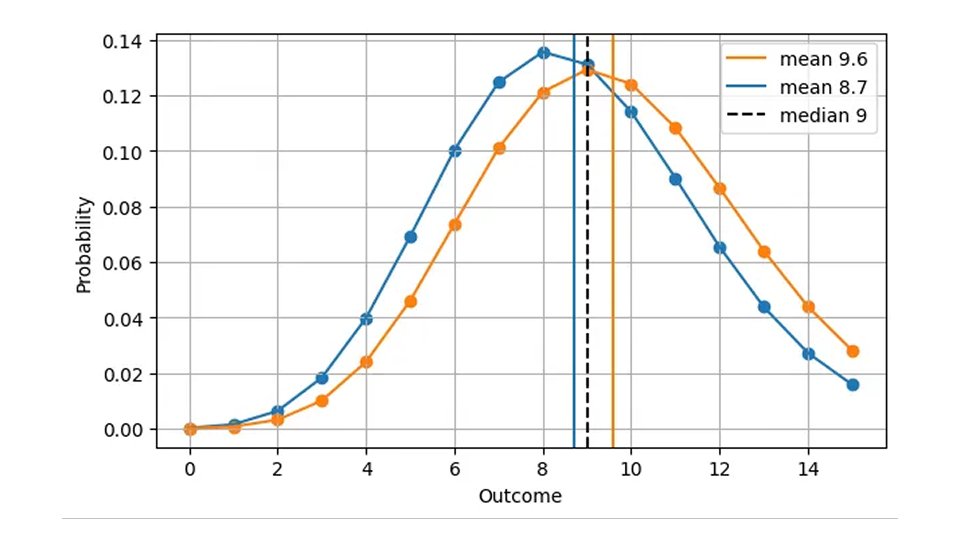
这在操作上是合理的:在这两种情况下,正确的做法是在某一天备有 9 种商品。因此,下图是第一幅图(AE 与预测值的函数关系)的一个更现实的版本。
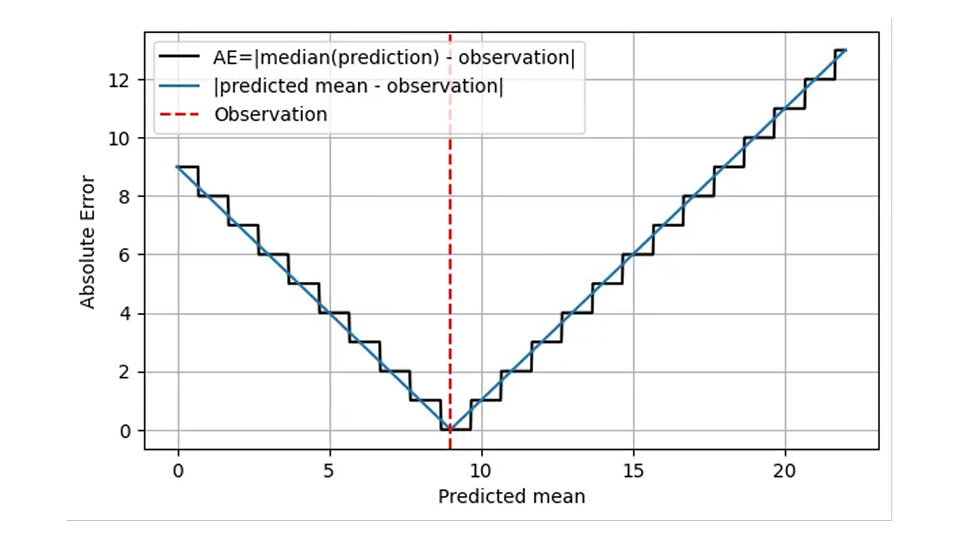
AE 是使用预测值的中位数(黑线)计算的,并且只假设整数值。关于 x 轴的含义,我说得更具体一些:不只是 "预测",而是预测的平均值。
这种阶梯形状意味着 AE 是粗粒度和不精确的:我们可以用肉眼分辨出平均值为 8.7 和 9.6 的分布,但 AE 无法做到!超过一定临界值后,仅凭 MAE 无法帮助您提高预测精度,而对于缓慢移动的项目来说,MAE 是非常重要的:1.7 和 2.6 之间的相对差异为 53% ,而预测值为 1.7 和预测值为 2.6 的 AE 是一样的!这种粗粒度行为会带来令人讨厌的跳跃,即分布中值从一个整数值跳跃到下一个整数值时出现的不连续性。在操作上,对某一天、某一地点和某一物品预测 1.7 或 2.6 没有区别:不过,预测也可用于更高层次的规划。在如此高的水平上,人们确实会注意到 1.7 和 2.6 之间的差别:在接下来的 100 天里,向供应商订购 170 件还是 260 件产品,会产生巨大的差别。
当每个预测时间段的预测平均值低于 0.69 时(慢速预测),绝对误差最佳的预测值为 0。非常明显的是,尽管我们经历了两个数量级,但 0.6、0.06 和 0.006 的预测绝对误差是相同的!在供应链中,"0 "预测毫无用处,因为你会进入完美 "0 "预测的恶性循环:你囤积了 0,你又卖出了 0,而你之前预测的 0 却完全正确。













