在第 1 部分中,我们对评估平均绝对误差的常规方法提出了质疑,这种方法只是求出预测平均值与观测结果之间的差值。我们发现,有必要使用正确的点估计,即中位数,用一个数字来概括分布,这与 "绝对误差 "的操作解释是一致的。不过,这也带来了 MAE 一些令人不快的特性:粗粒度、不连续、对慢速移动者毫无用处。
为排名概率得分扫清障碍
显然,我在本博文第一部分给大家留下的情况并不令人满意:对于预测均值低于 0.69 的慢动作选手来说,MAE 是不连续的、不精确的,甚至是无用的。尽管如此,其合理的商业解释--成本与误差成正比--仍然具有吸引力。我们能修好吗?
我们能不能不要用中位数,而改用其他总结,比如更友好的平均值?遗憾的是,假装中位数/平均数的区别无关紧要并不能使其变得无关紧要。走这条路并不能解决我们的问题,反而会带来新的问题:在 MAE 评估错误的情况下获胜的预测将是有偏差的。
既然我们被中位数束缚住了,作为一个总结,我们还有什么可能改进 AE 呢?有一个方面我们可以改变,即 "总结 "和 "计算误差 "这两个过程的顺序。目前,我们首先进行总结(分布映射到点估计器),然后计算误差("点估计器 - 结果")。让我们深吸一口气,将这两个步骤互换一下,如下图所示(左侧):给定一个预测分布(红色)和一个观察结果(蓝色),让我们计算每个预测结果的 AE(黑色箭头):
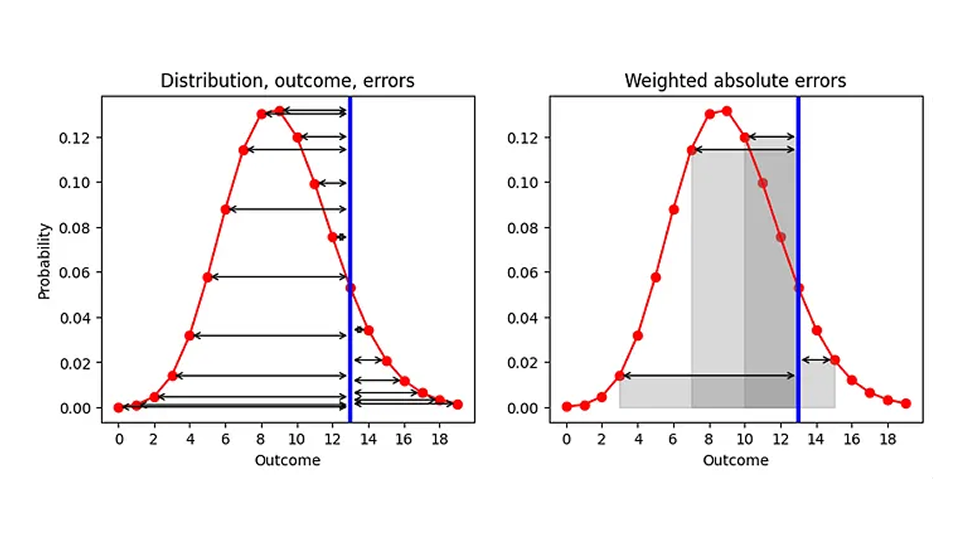
结果是一个 AE 列表,每个结果有一个 AE(包括与实际结果一致的预测,AE 为 0)。由于我们的目标是取代 AE 这个单一的数字,因此我们需要对这些众多的 AE 进行汇总。让我们取平均预期结果的平均值,并将我们分配给每个结果的概率作为该平均值的权重。从几何角度看,我们是将误差箭头和 x 轴所围成的区域相加,如右图中几个结果所示。
对于数字与概率分布之间的距离来说,这个规定是一个合理的定义:您可以用分配给某个可能结果的概率来权衡与该结果的每个距离。作为一种边缘情况,如果分布在所有地方都为 0,但有一个结果的分布为 1(确定性预测预示这个结果一定会实现),我们就可以恢复传统的 AE:确定性预测结果与观测结果之间距离的绝对值。我们改进后的 AE 成为用于确定性预测的传统 AE!
我们可以用这个公式来表示处方:
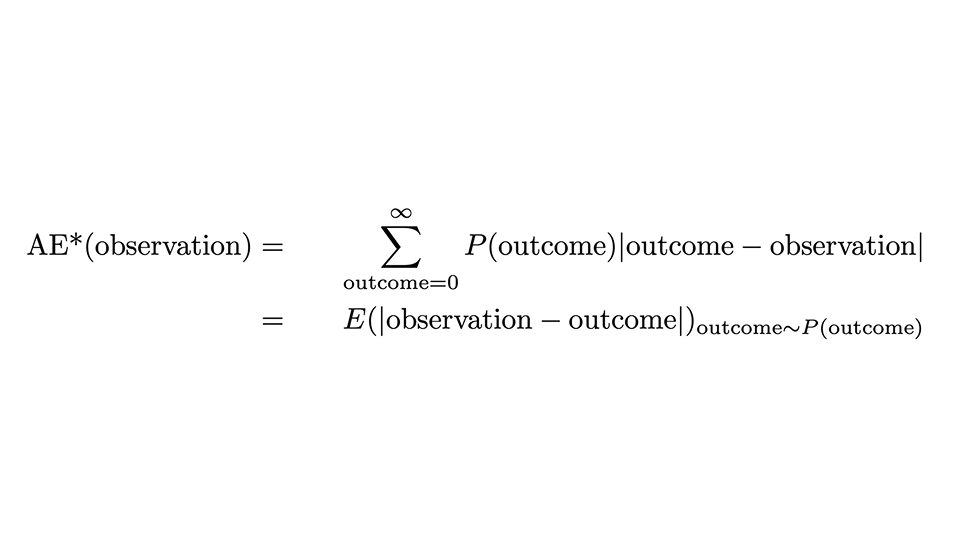
看起来确实有点吓人,但让我们轻轻地看一下:一个观测值的 AE*,即 "校正 AE",是该观测值的 AE,但它是所有可能结果的平均值(结果总和),预测概率 P(结果)作为权重。第二行表示,当结果按照概率分布时,这与观测值和结果之间绝对距离的期望值相吻合。
多么刺激的旅程我们还没到那一步,但也差不多了:AE* 并不完全是 "排名概率得分",而且我们还不知道这个累赘的名字是怎么来的。
上述定义的 AE* 有一个不理想的特性:当真实分布是具有一定平均值的泊松分布时,最低、最佳 AE* 并不是在匹配该平均值时实现的,而是在匹配一个稍小的平均值时实现的。如果您的预测在 AE* 中获胜,那么它很可能有偏差,预测不足。原因是分布的绝对宽度随平均值的增加而增加,这有利于较小的平均值(这又是一次宣传以前博文的机会[链接到《预测少有不同》1&2])。这个问题是可以解决的:我们需要减去分布的预期宽度的一半,也就是从预测分布中抽取的两个随机结果之间的预期距离。最后,我们就得到了排名概率得分:
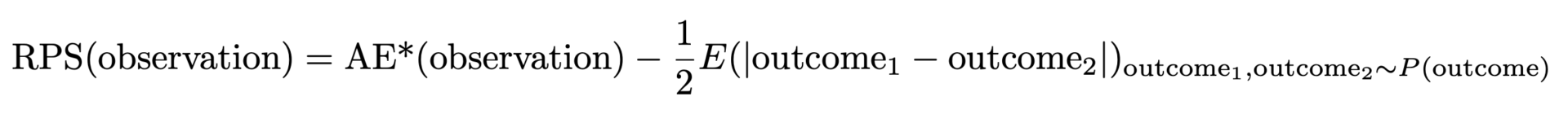
但为什么这叫 "概率排序得分"(RPS),为什么它如此不受欢迎?通常通过包含大量概率、阶跃函数和累积概率的抽象公式来介绍 RPS。如果你对概率论和统计学感兴趣,这种纯粹的概率论解释就很有意义,但对于实际工作者来说,这种解释仍然是难以理解的。我们的 "改进型 AE "和概率论的两种提法不谋而合,这确实很了不起:丑小鸭(在实践者眼中)变成了美丽的天鹅。
排序概率得分如何解决平均绝对误差的缺陷
我在这篇文章的第一部分就指出,MAE 具有不方便的特性:它粒度粗、不连续,对慢动作者毫无用处。改进后的 MAE "RPS 是否能解决这些问题?的确如此!
在下图中,RPS(黑线)与 AE(蓝线)进行了比较,观测值同样为 9(红色虚线)。对于远离结果 9 的预测,RPS 和 AE 的表现类似,RPS 只是略低于 AE。当预测的平均值和观测值重合为 9 时,AE 的命中率为 0,而 RPS 则持怀疑态度:由于 RPS 知道分布情况,它认为结果正好与预测分布的中位数相吻合也可能是偶然的:因此,RPS 从未触及 0:没有任何一个结果可以明确地证明概率预测是正确的。当偏离结果 9 时,AE 是严格的,会立即对 "偏离 "进行惩罚,并付出相应的代价。RPS 在这方面比较仁慈,不会像 AE 那样快速增长,这反映出 "有点偏差 "可能是运气不好,不需要立即受到制裁。这更符合企业的实际情况:运营计划通常是可以容忍轻微偏差的。每个人都希望,但没有人会认真地期待一个确定性的预测,而且有安全库存来考虑这一点。一旦偏差增大,就会产生实际成本。
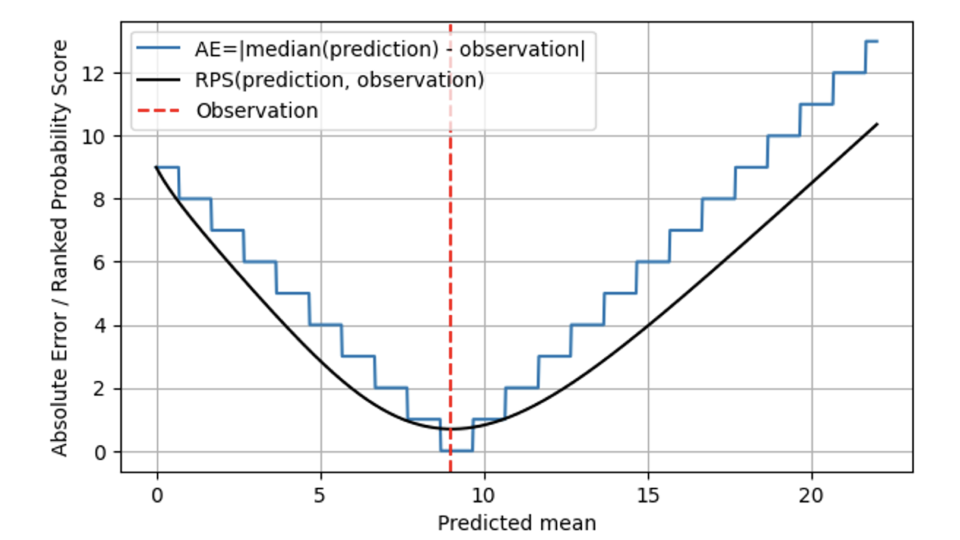
总体而言,排序概率得分不会在不同值之间 "跳跃",但从数学上讲,它在预测平均值上是连续的。就 AE 而言,8.7、9.3 和 9.6 的预测值没有区别,但就 RPS 而言,它们确实有区别:当预测平均值为 9 时,RPS 正好达到最小值。
对于滞销产品,RPS 有帮助,但不是灵丹妙药:即使使用 RPS,也很难区分 100 天销售一次的产品和 200 天销售一次的产品。不过,即使是 0.6、0.06 和 0.006 等较小的不同预测值,RPS 也会假设不同的值。
RPS 有助于解决 MAE 的许多问题,但有一项挑战即使是 RPS 也无法解决:不可避免的比例缩放使得慢速销售者和快速销售者表现出不同的行为。不过,使度量具有扩展意识的方法(本博客[链接到《预测少有不同》1&2]中的部分内容)可以以应用于 AE 的相同方式应用于 RPS。与相对 MAE 相比,相对平均 RPS(平均 RPS 除以平均观测值)在该图中的形状要平滑得多,显示了两个指标的最佳可实现值:
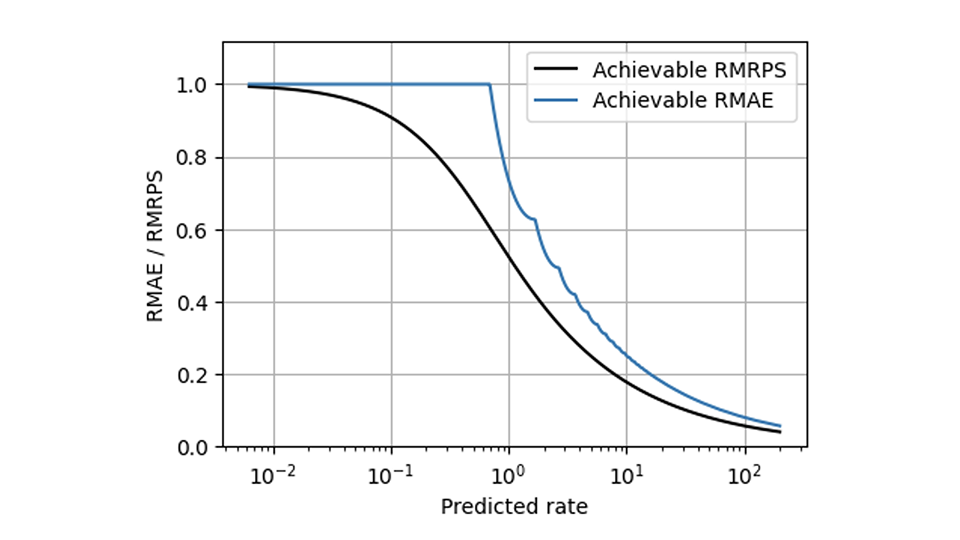
什么时候应该使用 MRPS 而不是 MAE?
有意义的预测从来不是确定的和肯定的,而是概率的和不确定的,这需要在评估中加以考虑。说人类不喜欢不确定性是非常轻描淡写的说法:人类讨厌不确定性。人们愿意牺牲大量的预期效用来实现完全的确定性(当风险是致命时,这样做是合理的)。当企业利益相关者被告知预测 "只 "提供概率预测时,他们往往希望得到确定性预测,而预测人员需要拒绝做出这样的预测,让他们失望。但是,明确指出不可避免的不确定性并不是软弱的表现,而是值得信赖的表现。
概率分布包含了每种可想结果的概率,将概率分布的全部表达能力浓缩为一个数字,看似简单、粗略、粗糙,但这正是你在储备物品时必须做的事情。因此,从概念的角度来看,"排序概率得分 "比 "绝对误差 "能更好地回答 "结果与预测相差多远 "的问题。
只要预测的概率性质无关紧要,AE 和 RPS 之间的差异就可以忽略不计,AE 和 RPS 可以交替使用(前者比后者更容易计算,后者假定的数值略小)。也就是说,当概率分布的宽度远小于典型的误差时,作为预报员,我就不能把出现的误差归咎于 "无法避免的噪音,而对此却无能为力"。例如,当我预测某些商品能卖出 1000 次时,我并没有特别的雄心壮志,当结果在 800 到 1200 左右时我就已经很高兴了,这时使用 RPS 和 AE 的区别就变得微不足道了。为了简单起见,我应该坚持使用 AE。
每当我们触及中慢速移动系统时,也就是当我们预测平均值为 0.8、7.2 或 16.8 时,是将分布浓缩为一个单一的数字来评估 AE,还是使用 RPS 进行稍微复杂的评估,就会产生不同的结果。在预测 "1 "时,我们的意思是观察到 "1 "的概率大约是 37% ,观察到 "0 "的概率也是 37 。因此,忽视中慢速销售机制中预测的概率性质是危险的,也是误导性的。但现在你知道如何考虑概率分布了:我希望你现在也能把它看作是预测评估野生动物中的美丽天鹅,它能让统计学家和实践者都感到满意。













