一视同仁--在一般情况下听起来不错,但在概率预测评估中并非如此
让我们回到之前的例子,谈谈苹果、金枪鱼罐头和瓶子。在这里,比较 APE 意义不大,原因有二。
顾名思义,慢销品的销售频率低于快销品。因此,与同样不可靠的快速销售预测相比,不可靠的慢速销售预测对业务的影响要小得多。一些边际滞销品因缺货而损失 5% 的销售额,对供应商来说只是不便,而畅销品损失 5% 的销售额则可能相当惊人。归根结底,绝对数字对您的业务至关重要。您高估了您的主要产品在美国的总需求量 20% ?您可能遇到了问题,需要处理大量未售出的存货,这甚至可能危及您的整个业务。您对图瓦卢同样产品的总需求预测过高了 20% ?我并不是针对图瓦卢(无意冒犯,真的!),但你也许可以放宽心,因为这个错误不会让你的生意破产。与您的面包& 黄油类别相比,您在小分类或市场中可以容忍更大的相对误差。为什么要将边缘项目或客户群体提升到与真正的大鱼同等重要的地位?
除了这种明显的差异(小就是小,大就是大)之外,还有一种看似微妙却很重要的统计效应:可实现预报准确率的规模依赖性。对于每天销售 10 次的产品来说,即使是完美预测(具有泊松不确定性),有时也难免会出现 10% 的偏差。每天销售 10000 次的产品打折 10% ,这显然说明了一个问题。慢销品不仅在业务上不如快销品重要,而且其相对误差自然也更大,这在之前的博文《 预测少有不同》第一部分 和 第二部分 中有更详细的论述 。
就上述食品杂货预报而言,你可能只是运气不好,碰上了当天的金枪鱼。多出的 16 瓶水似乎就不那么情有可原了。因此,绝对百分比误差 (APE) 不能很好地反映可实现的预测质量,无论是在业务方面(它对不平等的事情加权相同)还是在统计方面(其可实现值需要预测值本身的背景)都是如此。
以 MAPE 管理补货会导致灾难性的库存水平
换句话说,MAPE 本身并不是预测质量的良好指标:在三种不同情况下,是否达到 20% 、70% 、90% 并没有直接的解释意义。在 MAPE 值一定的情况下,我们不应该妄下结论。但是,即使 MAPE 值本身对模型的整体质量几乎没有任何影响,您仍然可以预期,在特定的预测情况下,MAPE 值获胜的预测应该是最好的预测。正如我现在要解决的问题,你也需要放弃这种较弱的期望。
考虑一家提供多种不同产品的超市--从每季度销售一次的慢销品到每天销售 100 次的快销品。物品的补给由一个系统完成,该系统会选择每日 MAPE 最佳预测,并根据预测进行预购。也就是说,它会选择 MAPE 最小的预测值。该超市的业绩如何?
为了简单起见,请关注 5 种典范产品:苹果、香蕉、腰果、火龙果和茄子:苹果、香蕉、腰果、火龙果和茄子的真实平均日销售率分别为 0.01、0.1、1、10 和 100:最慢的苹果大约每季度销售一次,最快的茄子每天销售 100 次(如果你怀疑这些数字不是为了现实世界的合理性而编造的,而是为了数学上的清晰和简单,那你是对的)。在这个思想实验中,我们知道这些销售率,它们是对每种产品的最佳预测。利用泊松分布,我们可以模拟发生的情况,以及具有最佳 MAPE 的预测值是多少。
下表列出了每种产品的真实销售率(即无偏差的最佳每日预测)、模拟 MAPE、优化 MAPE 优胜预测、模拟 MAPE 以及由此产生的偏差:
| 产品 | 真实的每日销售率,无偏见的每日预测 | 真实销售率的 MAPE | 获 MAPE 优胜的每日预报 | 获胜预测的 MAPE | MAPE 优胜预测的预测偏差 |
| 苹果 | 0.01 | 99% | 1 | 0.25% | +9,900% |
| 香蕉 | 0.1 | 90% | 1 | 2.5% | +900% |
| 腰果 | 1 | 23.3% | 1 | 23.3% | 0% |
| 火龙果 | 10 | 31% | 9 | 29% | -10% |
| 茄子 | 100 | 8.11% | 99 | 8.05% | -1% |
请记住,真实的日销售率无疑是补货系统的最佳输入值,因为它是预期销售额的平均值。如果补货使用 MAPE 优胜预测,会发生什么情况?超市过度储存滞销品:每天补充一个苹果、一根香蕉和一个腰果,但苹果每 100 天才能卖出一个,香蕉每 10 天才能卖出一个!苹果和香蕉堆积如山,腰果也不错,但火龙果的需求却得不到满足:平均有一位顾客想买火龙果,但没买完就走了。对于快速流动的茄子来说,1% 的误差也许是可以原谅的--然而,令人吃惊的是,"最佳 "预测总是有偏差的,除非真正的销售率等于 1。
上表中计算的数字假定了一个完美的世界,在这个世界中,预测人员喜欢使用泊松不确定性最小的模型。对于一个更现实的模型来说,如果存在一些适度的额外不确定性(技术上说:过度分散),情况马上就会变得更糟:
| 产品 | 真实的每日销售率,无偏见的每日预测 | 真实销售率的 MAPE | 获 MAPE 优胜的每日预报 | 获胜预测的 MAPE | MAPE 优胜预测的预测偏差 |
| 苹果 | 0.01 | 99% | 1 | 0.3% | +9,900% |
| 香蕉 | 0.1 | 90% | 1 | 3% | +900% |
| 腰果 | 1 | 25% | 1 | 25% | 0% |
| 火龙果 | 10 | 73% | 6 | 53% | -40% |
| 茄子 | 100 | 49% | 72 | 40% | -28% |
按真实销售率计算的 MAPE 值与 MAPE-获胜预测的 MAPE 值之间的差距大幅拉大。换句话说,用户可能会认为 MAPE 优胜预测的 "证据 "比上面的还要充分。然而,与理想情况相比,MAPE 最佳预测偏差更大:目前,火龙果和茄子的预测不足率分别为 40% 和 28%--这将导致大量缺货。下面,我们将了解为什么更多的不确定性意味着 "我们需要稳妥行事",以及为什么这意味着 "我们需要低调行事"。
显然,采用这种策略的超市不会长久生存下去!因此,MAPE 的问题不仅仅是业务可解释性(它不适合回答 "预测有多好?)但有可能导致严重的运行问题(选择无可争议的较差预报而不是较好的预报)。让我们来探究一下原因!
MAPE 普查零计数事件,带来灾难性后果
在计算 APE 时,当实际值为零时,我们会遇到很大的麻烦,因为我们需要除以实际值。这样,APE 就没有定义,也就无法计算 MAPE(记住,它是所有 APE 的平均值)。也就是说,零销售事件会直接从数据中删除。这些数据的移除效果和感觉一样糟糕:在 MAPE 最佳预测中,它会导致对超级慢动作(每个时间段销售一次或更少)的公然过度预测偏差:由于 0 事件被忽略,因此对任何产品、地点和日期的最低合理预测值都是 1,即使是每年销售一次的产品也是如此!由于经过 MAPE 优化的预测可以安全地忽略结果 "0",为了安全起见,建议将 "1 "作为最低预测值。清除的替代方法(如% 而不是删除)并不能解决这个问题:结果为 0 的 1.7 预测显然比结果为 0 的 17,000 预测问题要小;给这两个事件分配相同的人工 APE 是没有意义的。也就是说,只要你的数据可能包含 "0 "作为任何事件的实际值,MAPE 就会出现极大的问题。优化它将导致对超慢移动项目的预测过高,正如我们在表格前两行看到的那样。
MAPE 对预测不足和预测过高的惩罚不同,导致估算偏差
预测 1,观察 7:APE 约为 6/7。86%.你觉得太多了吗?如果是这样,交换数字,预测 7,观察 1:您的 APE 变成 6/1,600% !APE 对高估某一系数的惩罚要比对低估同一系数的惩罚重得多。对于预测不足的情况,最坏的 APE 可能是 100% ;对于预测过高的情况,APE 是无限制的。因此,只要你对结果不确定(你永远都不应该不确定,每个好的模型都知道自己在某种程度上的不确定性),安全的做法就是低估:不惜(几乎)任何代价避免强烈的过高预测,而大量的过低预测也不会让你的脖子断掉。因此,即使在预测不确定性最小的情况下(我们在第一张表中假设了这一点),MAPE 最佳预测对销售率超过 1 的预测也是偏低的(最后两行)。此外,训练数据的变异性越大,模型的不确定性就越大,MAPE 最佳预测的低估程度也就越大:请记住,安全就是低估,不确定性越大,就越要安全,MAPE-最优预测也就越低。这种对冲过高预测的做法导致了第二张表格最后两行的强烈偏差。修正的 MAPE 可以解决这种不对称问题:例如,可以根据预测值和实际值的平均值计算误差百分比,而不是仅根据实际值计算误差百分比--但这些修正并不能完全解决不对称问题,还会引发其他问题和悖论。
MAPE 表现出特别复杂的缩放行为,让我们不知道预测到底有多好
诚然,缺乏可解释性(50% MAPE 是好是坏?)并不是 MAPE 的独有特征:每个指标都与规模有关,对慢速和快速移动者而言,其值也不同。然而,由于上述两种效应的共同作用,MAPE 的缩放尤其错综复杂:一方面,MAPE 最佳预测永远不会输出小于 1 的数字,我们只需去除 0 的销售结果。另一方面,销售率越高,相对误差越小。在这幅图中,我们显示了 "安装 MAPE",即作为销售率函数的最佳可实现 MAPE。
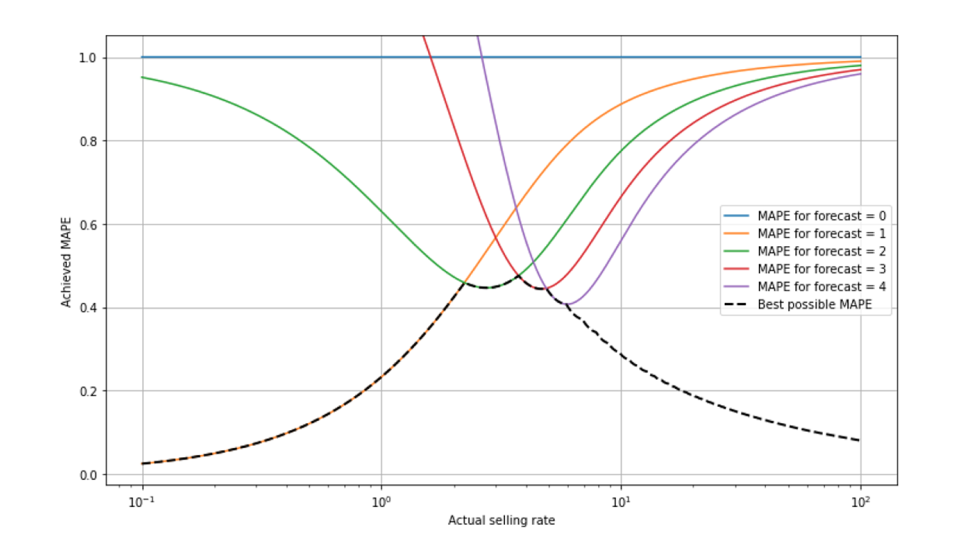
深吸一口气,让我来解释一下你所看到的:x 标度是对数,因此我们可以很好地观察到小额销售率--标度从 0.1 到 100,从超慢到超快。对于低于 2 左右的小卖出率,预测值为 1 是最好的,它产生的 MAPE 值由橙色线给出,橙色线从左下方(由黑色虚线覆盖)一直延伸到右上方。预测 2 将导致慢动作(绿线)的 MAPE 偏大,接近 95% ,卖出率为 0.1。预测结果为 0 时,MAPE 始终为 100% (蓝线):对于任何不为 0 的结果(这些结果已从评估中剔除),我们有 APE=|actual-0|/actual=100% 。在销售率约为 2.3 时,预测 2 成为最佳预测,因此黑色虚线(最佳 MAPE)从橙色跳到了绿色。每当最佳预测值从一个值跳到下一个值时,它就会进一步轮换(预测 3 和预测 4 分别用红色和紫色表示)。
当我们研究移动速度非常慢的项目时(向左),最佳 MAPE 会降低:由于 0 次销售事件已从数据中删除,"幸存 "的事件大多是 1 次销售事件,而且商品销售速度越慢,"幸存 "的事件就越多。对于 0.1 的销售率来说,单日售出 2 件商品的可能性已经很低,因此,在大多数非 0 的情况下,预测 "1 "是完美的,实现的 MAPE 也相当低。换句话说,当你知道数据中的 "0 "会被删除,而项目的速度又很慢,那么 "1 "就是一个非常安全的销售数量赌注。对于 1 到 5 左右的中等大小数值,我们可以看到最佳 MAPE 的 "转折"。对于 10 或更高的大预测值(图中右侧),可实现的 MAPE 再次下降:在大比率的限制下,泊松分布变得相对狭窄(参见我们之前的博文《预测少有不同》1&2)。
我真的尽力解释了 "安装 MAPE "的形状!我用了两段 300 多字,但恐怕并不完全成功:你的理解是否使你今后能够在预测销售率的背景下直观地判断 MAPE?如果您觉得不会--不用担心:这种复杂性是另一个微不足道的论据,说明即使在专业人士中,也不太可能广泛传播对 MAPE 值的直观正确判断。
MAPE 最佳预测与业务无关,危及潜在预测价值
在许多应用中,在 MAPE 上获胜的预测并不是您所希望的无偏预测。那么,"优化 MAPE "又是什么意思呢?在数学上,最小化 MAPE 的值是最小化一个看起来很麻烦的表达式,我甚至不敢在一篇不是针对统计学家的博文中写下这个表达式。你需要知道的是这一表述没有任何有意义的商业解释。无论您想通过预测达到什么目的--确保供应、减少浪费、计划促销和降价、补充物品、计划劳动力......--在您的应用中,错误预测的商业成本肯定无法通过 MAPE 反映出来!理想情况下,选择一个能够反映 "预测失误 "实际财务成本的评估指标。你要优化的不是抽象的数学函数,而是最大化业务价值。
另一种选择:让指标直接反映业务
除了按国家和强假设预测 GDP 等情况外,MAPE 既不适合用来表示预测模型的好坏(由于缩放),也不适合作为在两个相互竞争的模型中进行选择的决策驱动因素(MAPE 获胜的预测是有偏差的)。还有什么选择?最理想的情况是,所使用的指标能直接反映业务价值。平均绝对误差(MAE)量化了库存过量的成本与缺货的成本相同的情况,这是一个很强的假设,但肯定比 MAPE 更接近现实。MAE 与预测本身具有相同的维度("项目数"),因此在很大程度上取决于规模。将 MAE 除以平均销售额,我们就得到了相对平均绝对误差 (RMAE),由于泊松分布的比例特性,RMAE 也不是与比例无关的。因此,规模依赖性总是需要明确解决的。
然而,仅仅忽视最佳 MAPE 估计值存在偏差是不行的:重要的战略决策取决于可靠、有意义、与业务相关的预测评估!是选择软件供应商 A,还是选择软件供应商 B,抑或是我们的内部解决方案?我们应该把改进模型的重点放在哪些品种上?这一新类别中的预测 "足够好 "吗?预测评估应提供清晰、高水平、可解释、反映业务的证据,以回答这些问题和许多其他问题。MAPE 对此无能为力。















