Calibration and sharpness

博客

校准和清晰度：预报质量的两个独立方面

  • Calibration and sharpness
3 分钟阅读

什么是好的预测？

预测就像朋友：信任是最重要的因素（你永远都不希望你的朋友对你撒谎），但在你值得信任的朋友中，你更愿意结识那些能告诉你最有趣故事的人。

 

我这个比喻是什么意思？我们希望预测 "好"、"准"、"精"。但这是什么意思呢？让我们理清思路，更好地阐述和想象我们希望从预测中得到什么。衡量预测质量有两种独立的方法，您需要同时考虑这两种方法--校准和清晰度--才能对您的预测性能有一个满意的了解。

预测校准

为简单起见，让我们从二元分类开始：预测结果只能有两个值，即 "真或假"、"0 或 1 "或类似值。

更具体地说，让我们来看看电子邮件，以及它们是否会被邮箱用户标记为垃圾邮件。预测系统会为每封邮件计算出该邮件被用户视为垃圾邮件的概率百分比（我们将其视为基本事实）。超过一定的阈值，如 95% ，电子邮件就会被放入垃圾邮件文件夹。

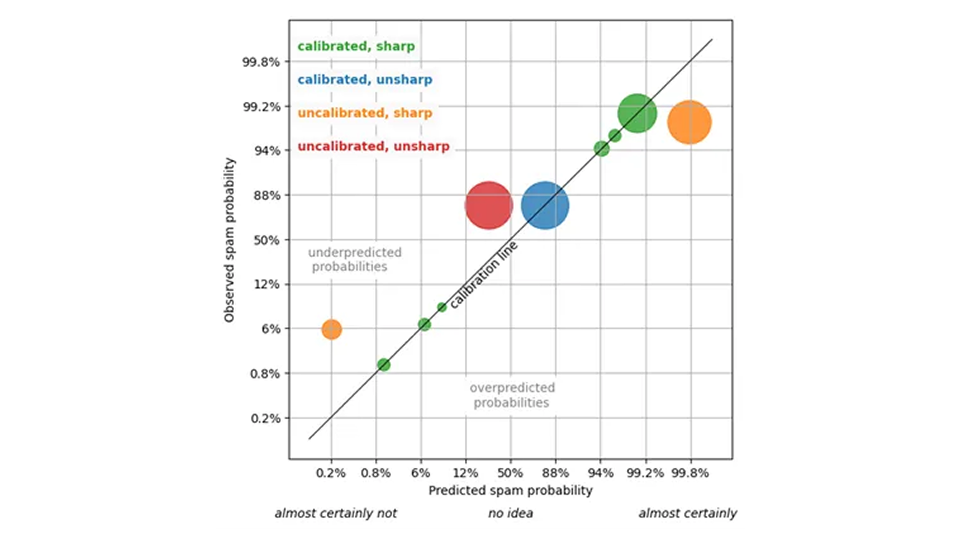
要评估该系统，首先可以检查预测的校准情况：对于那些被指定为垃圾邮件概率为 80% 的邮件，真正的垃圾邮件比例应该在 80% 左右（或至少在统计上没有显著差异）。对于那些垃圾邮件概率被定为 5% 的邮件，真正的垃圾邮件比例应该在 5% 左右，以此类推。如果是这样，我们就可以相信预测：所谓的 5% 概率确实是 5% 概率。

经过校准的预测可以让我们做出战略性决策：例如，我们可以适当设置垃圾邮件文件夹的阈值，还可以预先估计误报/漏报的数量（有些垃圾邮件会进入收件箱，而有些重要邮件最终会进入垃圾邮件文件夹，这是不可避免的）。

预测清晰度

校准是预测质量的全部吗？不完全是！试想一下，如果对每封电子邮件都进行总体垃圾邮件概率预测，即 85% 。这一预测非常准确，因为 85% 的电子邮件都是垃圾邮件或其他恶意邮件。你可以相信这种预测，它没有骗你--但它非常没用：您不能根据琐碎的重复声明 "这封邮件是垃圾邮件的概率是 85%"做出任何有用的决定。

一个有用的预测是对不同的电子邮件赋予截然不同的概率--你老板的电子邮件的垃圾邮件概率为 0.1% ，可疑的医药广告的概率为 99.9% ，并保持校准。统计学家把这种有用性称为锐度，因为它指的是预测结果分布的宽度：越窄，越尖锐。

非个性化预测总是产生垃圾邮件概率 85% ，是最大限度的不清晰。最大清晰度是指垃圾邮件过滤器对每封电子邮件只赋予 0% 或100% 的垃圾邮件概率。这种最大程度的敏锐性--确定性--是可取的，但却不现实：这种预测（很可能）没有经过校准，一些标记为 0% 垃圾邮件概率的邮件会变成垃圾邮件，一些标记为 100% 垃圾邮件概率的邮件会变成你重要伴侣的邮件。

最佳预测是什么？我们不想放弃信任，因此需要对预测进行校准，但在校准后的预测中，我们希望得到最准确的预测。这就是 Gneiting、Balabdaoui 和 Raftery 于 2007 年提出的概率预测范式（J.P.D.，2007 年）。R.统计学家Soc.B 69, Part 2, pp.243-268):最大限度地提高清晰度，但不要影响校准。 在保持真实的前提下，尽可能做出最有力的陈述。就像我们的朋友一样，给我讲最有趣的故事，但不要对我撒谎。对于垃圾邮件过滤器来说，最敏锐的预测值为：1% ，相当明显不是垃圾邮件的邮件为 99% ，难以判断的情况（应该不会太多）为中间值。

重新调整供应链

每月通过《供应链指南针通讯》提供全球趋势和行业见解。 

立即注册

校准和锐度的抽象画

让我们从下图中直观了解垃圾邮件分类器的校准和清晰度。垃圾邮件分类器由一系列相同颜色的圆圈组成，每个圆圈的大小反映了被标记为相应预测垃圾邮件概率的邮件数量。x 轴是预测的垃圾邮件概率，y 轴是出现垃圾邮件的频率。选择坐标轴的方式是为了详细列出接近零（"几乎肯定不会"）或接近一（"几乎肯定"）的概率。

当一个圆位于校准线（即预测概率和测量频率相匹配的对角黑线）上时，该圆就被校准了。圆离校准线越远，预测值与实际值之间的差异就越大，预测值就越未经校准。当圆圈位于校准线上方时，相关预测低估了真实概率；当圆圈位于校准线下方时，预测高估了真实概率。在右下角和左上角，你会发现一些灾难性的错误预测，这些预测把很大的概率赋予了罕见事件，反之亦然。

现在来看绿色圆圈：在所有六个圆圈中，预测概率和实际频率非常吻合，这反映了一个经过完美校准且相当敏锐的预测。单个蓝色圆圈是经过校准的（它击中了对角线），但它反映的是一种无用的、不清晰的预测，每次在被问及某封邮件的垃圾邮件概率时，它只会给出 "85%"。这是一种防御性预测：没有错，但没用。橙色圆圈反映了垃圾邮件过滤器过于自信：它生成的垃圾邮件预测值为 0.2% 或 99.8% ，这些都是很有说服力的说法，如果属实的话会很有用！然而，在 "几乎肯定不是垃圾邮件 "的电子邮件中，我们发现约有 5% 封垃圾邮件，远高于预计的 0.2% 。在 "几乎肯定是垃圾邮件 "的电子邮件（预测概率为 99.8% ）中，只有约 95% 最终成为真正的垃圾邮件。橙色预报比绿色预报更清晰，但失去了校准功能。表面上增加的确定性没有任何用处，因为我们无法相信预测。

红圈反映的是未经锐化和校准的预测：该垃圾邮件过滤器总是给每封电子邮件分配 "25%"的概率--这既是错误的（总体概率约为 80% ），也是不具体的。

"校准后的最大清晰度 "范例意味着，您要尽可能地将圆圈推到 "几乎确定 "的区域，即左下方和右上方，同时将它们粘在校准线上。我们的目标是 "1% 垃圾邮件 "或 "99% 垃圾邮件 "等强有力的、可操作的声明，而这些声明应该是真实的。

calibration-and-sharpness-body-01

需求预测的校准和清晰度

在 Blue Yonder，我们并不以过滤垃圾邮件为生，但我们确实会对客户需求等进行预测。我们的目标不是二进制（垃圾邮件/非垃圾邮件），而是一个数字。上述论证的大部分内容可以再次使用：一个经过校准但毫无用处的预测将总体平均需求量（产品、地点和天数的平均值）分配给未来的每种产品、地点和天数：对于一家典型的超市来说，"该产品明天的平均销售量为 1.6 倍"，对每种产品、每一天和每一个地点来说，都是一个真实的、经过校准的陈述，但对于补货或任何其他商业决策来说，却没有任何意义。另一方面，自诩为最敏锐的预测（"明天，在 123 号商店，你将卖出整整 17 根黄瓜"）是不现实的，会阻碍有关浪费和缺货的任何有意义的战略决策。

零售业预测可以变得多敏锐？在零售业，我们要面对许多潜在客户（每天多达 100 多位），每个客户都有可能以很小的概率购买某种产品：当你进入一家超市时，你只能购买其中的一小部分产品。如果我们再假设每种产品都有完美的可用性（永远不会缺货），而且每个客户最多只能购买一种给定产品，那么理论上最大可能的锐度就是已知的：这就是泊松分布，我们在上一篇博客 《预测》 中讨论过它的特性， 但很少有不同。也就是说，预测均值附近的销售分布遵循泊松分布：平均预测值为 "5 "时，真实需求量可能为 3（14% 概率）、4（18% 概率）、5（18% 概率）、6（15% 概率）、7（10% 概率）等。就像垃圾邮件过滤器一样，这些预测概率可以在实践中得到验证：当我们将 "13 根黄瓜 "事件的概率定为 12% 时，我们预计，平均而言，12% 这样的情况会导致 13 根黄瓜售出。在确定了校准之后，我们就可以利用预测结果做出战略决策，例如平衡缺货成本和浪费成本。

在实践中，泊松分布背后的有力假设往往无法实现：人们会购买更多的特定产品，产品会缺货，而且并非所有影响需求的因素都是已知的，这就使得假装知道平均购买概率变得难以捉摸。尽管如此，泊松分布仍然是一种近似的理想情况，尽管有时无法达到，但它提供了很好的指导。在我们的预测解决方案中，我们将实际取得的性能与不同的理论边界进行比较，以估计我们与特定情况下可能取得的性能有多接近。这有助于我们确定哪些是有待改进的成果，哪些是已经非常出色的预测，哪些是需要进一步调查的异常情况。

好的预测如何像好朋友

因此，"在校准的前提下最大限度地提高预测分布的清晰度"（Gneiting、Balabdaoui 和 Raftery）这一范式在任何领域都是非常有用的，它可以使预测性能有形化。最终，在每一种预测情况下，我们都希望能够自信地说这是一个尽可能精确的 校准预测。

这种预测就像你最有趣的朋友，他会给你讲精彩的故事，提供有用的建议，但从不对你撒谎。