在零售预测中,关注的数量是客户对某种产品的需求量,例如,有多少篮草莓被预订。在实践中,人们观察到的是一个略有不同但又有显著差异的数量,即登记销售额。销售量反映了需求量,但受制于生产能力,即库存水平:当需要 20 个篮子,但有 12 个篮子时,只能卖出 12 个篮子,而 8 个愿意购买篮子的客户却没有得到满足。销售和需求之间的区别看似毫不相干,但这篇博文将告诉你为什么把销售误认为需求会导致有偏见的培训和有缺陷的模型评估。您将了解有限库存如何影响销售,以及如何规避最重要的陷阱,自信地应对涉及有限库存的实际情况。
需求和销售
您能想到的最精确的预测是什么?您能下注的永远正确的需求预测是什么?在许多情况下,答案是:只需一直预测 "0 "即可!在需求预测为零的情况下,没有一件商品会被订购,没有一件商品会上架,没有一件商品会售出。结果证明,零预测是正确的,与观测到的零销售额完全吻合。这种绝对准确的预测显然不会让你的经理满意。
这个极端的例子说明,在提出要求时应该慎之又慎:零售商的目标不是做出精确的预测,而是经营可持续的业务。这一悖论也暴露了需求预测中的一个基本难题:预测本身会影响最终提供的库存量,从而影响对预测的评估。你可能会说,这种影响的存在是有道理的,预测就是为此而生的!但是,库存水平为可销售的商品数量设定了上限,这就人为地限制了可观察到的销售值。这就导致了假设需求量("需求多少")与观察销售量("销售多少")之间的差异。观察到的销售量是真实需求量还是可用库存量,取决于哪个更低。
在这篇博文中,我将让你相信,对需求与销售问题进行严格的概率处理是绕不开的。区分需求量和销售量、细致处理这些数量以及我们的准确预测和观察结果,是成功、正确地进行模型训练和评估的关键。
为了让事情具体化(和美味化),我们可以考虑一家销售一篮新鲜草莓的零售商。这样,售出的篮子的整数值就可以被视为 "件数"。遗憾的是,这些超新鲜的食品在白天不出售时就会被浪费掉。因此,过量订购,即库存多于需求,代价高昂,应予避免。另一方面,想象一下,你想买草莓,但当你在当地超市寻找时,草莓已经断货:你就成了一个心灰意冷的顾客,他的支付意愿没有得到满足。因此,订货不足,库存量少于需求量,无论是从客户满意度还是从收入和利润损失的角度来看,都是代价高昂的。
零售商应订购适当数量的草莓篮,仔细平衡浪费和销售损失。当然,要解决这个订购问题,必须有精确的需求预测,真正预测出有多少篮子被要,而不是有多少篮子被卖(还记得上面那个自我实现的 "0 "预言吗)。
我们能卖多少钱?
让我们深入了解一下需求预测,并剖析其含义。需求预测会告诉我们需要多少物品。但是,"需要 9.7 个篮子 "到底是什么意思呢?显然,一个人不可能卖出零头数量的草莓篮子,字面解释是荒谬的。尽管如此,我们还是接受并直观地理解了这一预测,并将其解释为对平均预期售出篮子数量的断言,即当相同情况重复多次时,我们平均售出的篮子数量(而且存量总是充足的,我们暂且假定如此)。因此,我们的预测隐含了某种概率分布,即某种关于销售 1、2、3......篮子的可能性的概念,因为它只说明了平均预期销售额。至于这些概率是多少,或者个别观测数据(即实际销售数字)与 9.7 的平均值有多接近,我们就不一一列举了。
让我们揭开隐藏概率分布的地毯,看看它应该是什么样子。我们将用下面的图表来举例说明。先验地看,期望值为 9.7 的概率分布可以呈现出截然不同的形状:左图所示,遇到 0 的概率为 51.5% ,而找到 20 的概率为 48.5% 。这样得出的平均值为 9.7,尽管我们从未观察到任何接近 9.7 的值,如 9 或 10,而只有极值,如 0 或 20。中间面板的概率分布中,10 的概率为 70% ,9 的概率为 30% ;它也带有期望值 9.7,但概率群更集中在接近均值的值上,从而成为典型销售数量的良好估计。均值为 9.7 的分布集合是无限大的,其中大多数分布都是乖离的(或数学家喜欢说的 "病态")。幸运的是,我们可以假设简单而良好的概率分布,例如右侧面板中的泊松分布(请阅读博文《预测少有不同》,了解为什么这是一个合理的选择)。
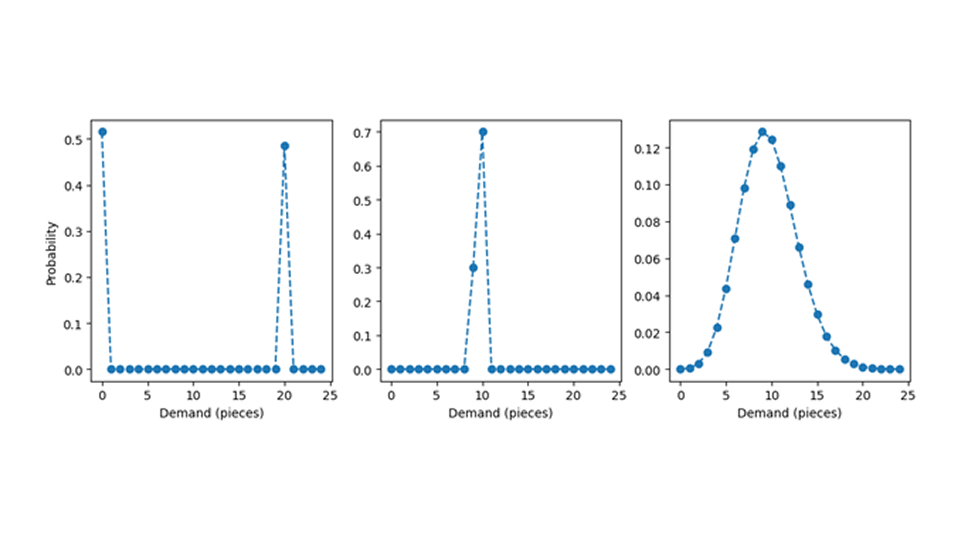
在本文中,我们假定预测产生的是泊松分布的平均值,而需求确实是泊松分布的,即预测是正确的。即使是这种理想化的情况,也会有很多错综复杂的问题,足以写一篇博文。
有限股票如何审查信息
现在,让我们欢迎有限能力加入游戏。给定需求分布后,我们将每个可能的需求值与由此产生的销售值进行映射,从而得到销售分布。对于所有低于或等于现有存货数量的需求值,需求量都会以 1:1 的比例转化为销售量:当有 12 个篮子可用时,要求 5 个篮子就会卖出 5 个,要求 12 个篮子就会卖出 12 个。当需求大于库存时,换句话说,当生产能力不足时,销售就会受到库存值的限制:当需要 13、25 或 463 个篮子时,只能卖出 12 个。当整个股票被抛售时,我们称之为 "产能冲击 "事件。然而,与 13、25 或 463 个篮子的需求相关的概率质量需要 "去到某个地方",它被有效地添加到总库存需求的概率中。下图显示了平均需求量为 9.7 和不同产能(16、12、8)下的销售概率分布。
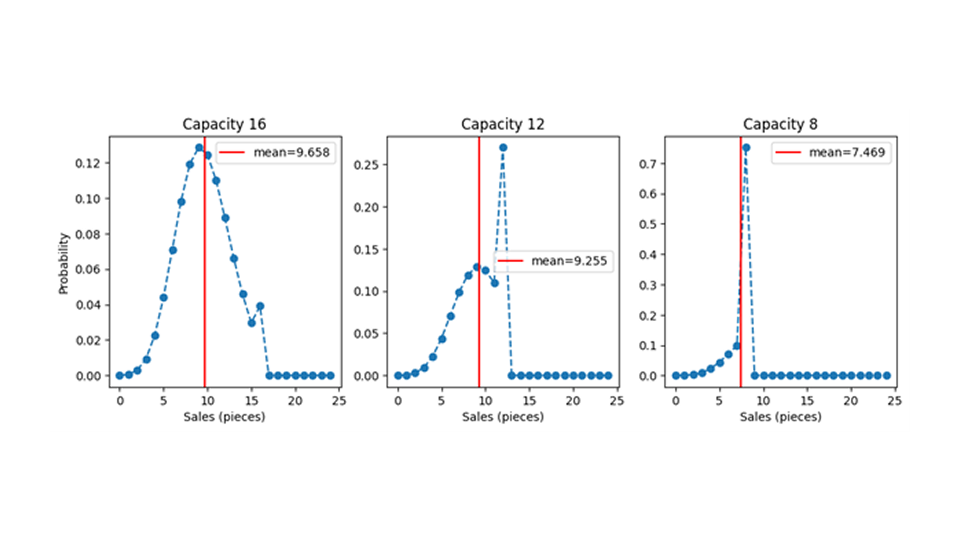
有限产能是对需求的审查,它消除了信息:当你设置了 16 个容量,并观察到一个容量命中,即 16 个销售量,你只能推断需求至少是 16 个,而不是 16、25 或 7624 个。实际需求量有某个你不知道的值,比如 47,但你只观察到 16。由于容量有限,我们正在以不可挽回的方式真正失去信息(不仅仅是客户满意度)。这种信息损失既增加了在有限容量下训练模型的难度,也增加了评估模型的难度。
图中还以垂直红线显示了预期平均销售额。也许令人惊讶的是,即使产能仍然大于预期需求,有限产能也会对销售预期值产生影响。也就是说,当你预测需求量为 9.7 时,你提供了 12 件库存商品,但平均销售量却低于 9.7!你需要比预测的平均库存量更多,才能卖出和预测的一样多!这可能会令人困惑:就单个活动而言,销售额只是需求和库存的最小值。但销售概率分布的平均值并不一定是预期需求量和产能的最小值,因为需要考虑概率分布的形状。之所以会出现这种可能令人惊讶的现象,是因为预测需求量的平均值依赖于平均值附近的波动,而这些波动在平均值上会相互抵消。也就是说,负波动(有时出售的商品少于 9.7)被正波动(有时出售的商品多于 9.7)所抵消。当容量有限时,这些必要的正波动就会被抑制,正负波动的抵消也就不再发生。即使产能大于平均预期需求,也会将平均预期销售额推低。
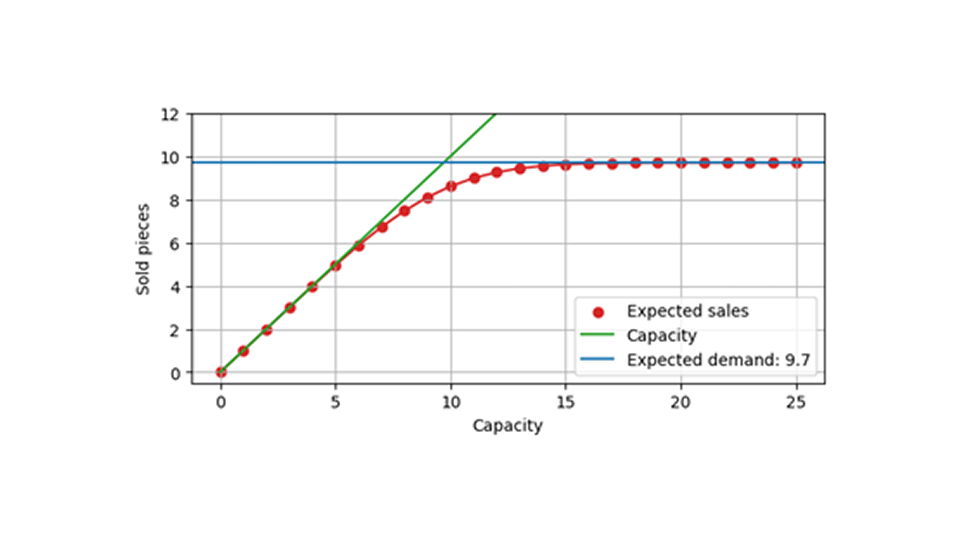
下图显示了预期销售额与生产能力的函数关系,同样是预期需求量为 9.7。当容量远大于预期需求时(如 20 左右),受有限容量影响的事件就很少发生。因此,预期销售数量未受影响,接近 9.7。当容量较小时,比如 5,那么几乎不可避免地会出现容量被占用的情况,平均而言,会售出一个接近该容量的值。在 7 岁到 14 岁之间,会出现一个过渡期,能力对销售额的影响很大,但不是完全决定性的。
对有删减需求的模型进行训练和评估
现在,我们已经掌握了我们的主力--销售概率分布,又称容量删减需求分布,让我们来了解一下在这种情况下训练和评估模型时需要注意什么。
我们需要区分不同的制度。如果每天都达到产能,人们就永远不会知道真实的需求量,而只能知道它的下限("我们卖出了 5 件,所以需求量至少是 5 件")。幸运的是,这种情况并不现实:当每天的生产能力都受到冲击时,我们就会面对大量不满意的顾客和大量无法满足的需求--任何零售商都无法长期维持这种运营模式。如果供应限制迫使它们这样做,它们可能会考虑通过提高价格来引导需求。
另一个极端是,当容量从未受到冲击时,我们就可以享受甜蜜的数据科学制度:我们每天都能读取真实的需求量,我们基本上可以忽略所有关于容量的讨论。但是,数据科学家的梦想却是可持续发展官员的噩梦:这种订购策略会造成大量浪费。鉴于预期需求量为 9.7,我们需要保持 21 种商品的库存,才能在 1,000 天内出现一次缺货。
因此,我们通常会遇到这样的情况:需求有时会达到产能(产品在一天中的某个时间点会售罄),有时则不会(晚上仍有一些库存)。这样做是合理的,因为在避免浪费和避免缺货这两个相互竞争的目标之间达成折中是可取的。
我们应该承认,建立尽可能好的模式与经营尽可能好的企业是有冲突的:在可持续发展的商业战略下(废物并非完全 "免费",但至少在一定程度上可以避免),产品有时缺货是不可避免的。然而,最好的数据科学是在保证永远不会发生缺货、每个销售值都能直接反映需求的情况下完成的。既然我们是在商业环境中进行数据科学研究,我们就必须面对中间情况和偶尔的缺货。













