预测评估陷阱

在本博文的第一部分，我们介绍了经过删减的销售概率分布。现在，让我们动手实践一下，看看有限容量在实践中意味着什么。我们首先指出一个人可能不经意间陷入的微妙陷阱，然后分享我们通常是如何解决这种情况的。

将销售误认为需求

你的经理可能会要求你完全忽略这篇博文，以获得 "第一个简单模型" "和 "对模型质量的粗略估计"。"你可能会深吸一口气，然后这样做，即直接将销售数字理解为真实需求。

会发生什么事呢？将无偏见的需求预测与观察到的销售额进行天真比较，通常会得出 "预测有偏差，预 测过高""的结论：有限的产能推低了观察到的销售值。越是频繁出现产能不足的情况，对销售的影响就越大。在实践中，尤其有害的是，有限产能对不同产品组的影响差别很大：为了避免浪费，生鲜产品时不时就需要断货，而产能也时不时就会受到冲击。非易腐食品通常以永不缺货的方式进行补充，而且几乎从未出现产能不足的情况。不同产品组之间的比较会因不同产能/库存战略的不同影响而大打折扣。

但是，我们是否能首先获得一个无偏的模型呢？这不太可能：在训练过程中，你的模型会直接学习到有偏差的需求。如下图所示，在平均值为 9.7 的完整需求分布中，模型只能学习受限的、有删减的分布，其平均值较低：

低估预测导致低订单，导致更多的缺货，导致更低估的预测，这种恶性循环不断加速运动，而评估却证实 "一切正常" ，"销售预测没问题"。"在其他情况下，培训和评估阶段的能力限制可能会因某种原因而不同，这对解释观察 到的偏差（或缺乏偏差）产生有害影响。

如果你已经读到这里，你可能已经明白销售额和需求量并不等同，你也能够说服你的经理采取更长远、更精确的方法。

选择未满足需求的日子

上述陷阱非常直观：需求量和销售量是不同的量，在两者不相等的情况下将其设定为相等显然是有问题的。我希望您避免的第二个误区比较隐蔽（预约两个小时的会议向您的经理解释）：项目中通常会出现的一种想法是，仅在无容量命中事件（即销售未达到容量饱和的那些日子）上对模型进行培训或评估。也就是说，在训练或评估中剔除了所有发生过删减（销售额等于存量）的事件，只保留低于容量的销售额。剩下的事件都是非受限事件，希望这样能使训练和评估不带偏见。

然而，事实并非如此！通过选择那些没有达到产能的日子，我们自然会选择那些需求量偶然特别小的负波动事件。也就是说，如果只关注那些负离群值事件，就会产生选择偏差。这样的培训或评估数据集不能公正地反映真实需求，反而会产生负面偏差。容量受影响的事件是指由于随机因素，真实需求量比平均值大一些的事件。这些事件对于记录一个无偏见的总体值是必要的。在下图中，我们可以看到为什么去掉产能受限事件会比在整个销售值数据集（即受限需求）上进行训练更糟糕：以未达到产能为条件的平均销售额（绿色虚线）低于整体平均销售额（红线），因为产能达到条件下的平均销售额（黑线）会带来更高的数值。请记住：我们希望学习的内容或预测的内容就是蓝色点状虚线的平均需求量。

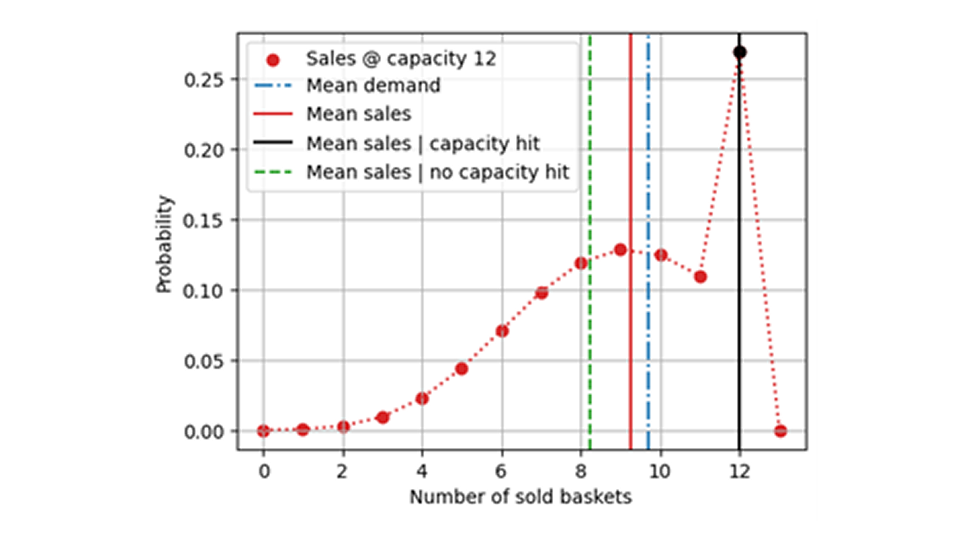
据统计，没有断货的日子并不能代表所有日子，但这些日子是进入超市的人较少的日子。也许是草莓不新鲜，也许是芒果的促销活动让人们走开了--无论如何，我们都是在选择异常值，不能指望这些异常值没有偏差！

如果您想采取相反的策略，选择那些达到产能的事件，那么您的数据集将会产生更大的偏差：这样一来，平均销售额就与预测完全无关了，因为它们完全再现了产能设置策略--销售额只是与产能始终匹配而已。

按照 "产能达到" "和 "产能未达到" "来分割评估数据，也违反了预测评估的一项重要原则：切勿根据预测时未知的标准分割数据。这种拆分几乎总是会在所产生的组别中引起微妙的选择偏差。博文《 你不应该总是知道更好》 中也讨论了类似的效果 。

如何避免陷阱

关于培训，结论是可怕的：没有办法绕过 "使用 Tobit 回归等方法进行适当的" 培训"，因为在容量为 12 时观察 12 只会为当天的真实需求设定一个下限。换句话说，我们需要一种回归方法，"了解" 12 件已售商品意味着 "需求 12 件或更多商品"。"有限产能真正删除了信息--使用产能受限的销售额作为输入的模型，即使这样做是正确的，也总是不如使用无约束需求的模型精确。

在模型评估中，我们可以明确考虑有限产能：可以根据删减概率分布计算出给定有限容量下的预期销售额。同样，请记住，产能限制下的预期销售额并不只是 "无限制需求预测" "和 "产能" "中的较小值，而是需要考虑全部限制概率分布。最后，我们可以进行如下比较：

在这种情况下，我们可以确认实际销售额（产能限制后）与预期相吻合。

预测容量命中概率和实际容量命中频率

尽管将产能限制下的预测销售额与实际销售额进行比较有助于确定预测的偏差（或缺乏偏差），并且是确定预测质量的良好的第一步，但我们经常会遇到一些类似以下内容的质疑："我们承认预测总体上没有偏差，但我们担心预测过高和预测过低都会导致不必要的浪费和缺货。"

换句话说，预测的相关方不仅对全球无偏见感兴趣，而且对每种可能的需求情况下的无偏见感兴趣。他们不希望在超级畅销的日子里预测不足，而在低迷的日子里又预测过高，以求平衡。尤其是，当产能受到冲击时，利益相关者希望确保只是轻微的冲击（只有少数客户的需求得不到满足）；当出现浪费时，浪费量不应巨大。

为了消除这种合理的担忧（你可以很容易地想象到，可怕的预测会在全球范围内毫无偏差，给你带来大量的浪费和不满意的客户），我建议按照预测的产能命中概率对数据进行分类。也就是说，给定预测和当天安装的一定库存水平，计算库存售罄的预测概率，即预测产能命中概率。当库存水平相对于预测值设置为较大值时，产能达到的概率接近于 0（例如，当库存水平设置为需求分布的 0.99-四分位数时，我们可以通过 99% 确定不会达到产能水平）。当库存量较小时，例如库存量设定在需求分布的 0.01 分位数时，产能命中概率接近 1。

对于每项预测，我们都有一个达到容量的预测概率（如 0.42）和实际达到容量的概率（达到或未达到）。这种单一的命中/不命中事件仅仅是轶事：仅仅存在几个 "不太可能的" 对"，"预测容量命中概率 = 0.05，但容量实际上命中了" ，并不意味着预测概率具有误导性。只有收集了许多概率预测和相关的命中/不命中事件，才能对预测概率进行严格验证。为此，需要收集多对容量命中概率（0 和 1 之间的浮点数）和容量命中（离散结果，1 表示 "命中" ，0 表示 "未命中" ）。将这些数据按预测的容量命中率分为 0 左右、0.10 左右、0.20 左右等几组。然后，计算每个容量桶的预测命中率和实际命中率的平均值。如果预测在 0.10% 的情况下会出现容量受限，那么我们预计在大约 10% 的情况下，容量会实际受限。

我们将预测概率称为 "校准后的" "，因为在 70% 的情况下，预测的 0.70 能力命中率是可信的（有关校准的更多信息，请参阅博文 " 校准与敏锐度"： 预测质量的两个独立方面 ）。通过校准预测，可以做出战略性补货决策：将库存水平设定为预计在 0.023 天内缺货，而实际缺货天数为 2.3% 。这就是风险管理：你以校准的方式量化风险，有意识地承担那些值得承担的风险。

在下图中，黑圈表示单个容量命中事件--容量命中（图上）或未命中（图下）。当我们将所有预测结果汇总在一起时，平均预测容量命中率为 0.82，与测量频率相符（绿色圆圈）。当我们按产能命中概率接近 0、接近 0.1、接近 0.2 等来区分时，我们会发现产能命中预测是经过校准的：蓝色圆圈接近对角线。

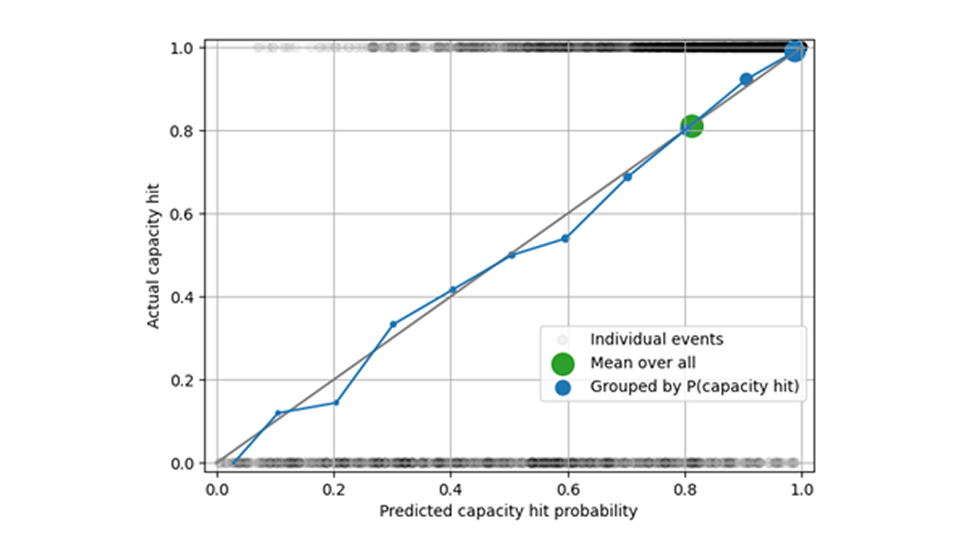
评估预测与实际产能命中概率和频率不足以确保良好的预测：当您备货 1,000 件物品时，预测 5 件、10 件或 100 件的产能命中行为没有任何区别--在所有情况下，事件最终都会被归入 "产能肯定不会命中 "的同一个桶中。"因此，对预测销售量偏差的分析应与运力命中率分析相辅相成，以验证预测在不同运力限制和速度下均无偏差。

一般来说，按照预测的产能命中概率或预测的销售额进行分组是遵循 "前瞻性：评估你所预测的，而不是向后看" "的规则，以避免博文《你不应该总是知道得更好 》中所描述的 "后见之明 "偏差。

结论：管理风险需要概率工具

点预测只预测一个数字，不适合处理战略性概率问题，如哪个库存水平能确保缺货率低于 1% 。当你提出一个概率问题时--所有关于风险的问题都是概率问题--你需要概率工具来回答这个问题。您需要教您的经理至少对 "期望值"、" "审查"、" 和 "分布 "有基本的了解。"

只要容量对现实世界产生影响（几乎总是如此），我们就必须认真对待容量限制。我们不应试图事后理解事件（"当天产能受到冲击，具体原因是什么？" ），而应向前看，通过预测销售额和预测产能受冲击概率对预测进行分类，从而评估预测的校准。

本博文中的所有示例都是在类似沙盒的环境中构建的，假定有完美的需求预测，会产生良好的分布。我为你们屏蔽了在现实世界中通常会遇到的所有更复杂的问题。不过，即使在这个简单的场景中，我们也能看到我们的直觉是多么容易被愚弄。因此，在解决评估问题时，不能一上来就按照自己的想法去做（"我们就按照命中容量和未命中容量来分组吧" ），而是要采取怀疑的态度，先模拟一下在理想情况下该方法会起到什么作用。